Question Number 10906 by niraj last updated on 01/Mar/17

$${Q}\:.\:\:{smallest}\:{positive}\:{x}\:{satisfying}\:{the}\:{equation} \\ $$$${sin}\mathrm{3}{x}+\mathrm{3}{cosx}=\mathrm{2}{sin}\mathrm{2}{x}\left({sinx}+{cosx}\right)\:,\:{is} \\ $$
Commented by niraj last updated on 02/Mar/17

$${sir}\:{answer}\:{please} \\ $$
Answered by ajfour last updated on 03/Mar/17
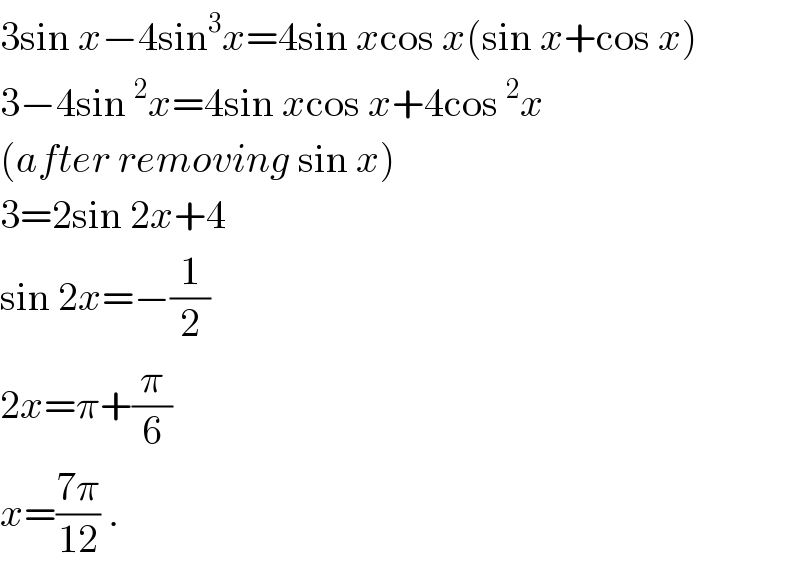
$$\mathrm{3sin}\:{x}−\mathrm{4sin}^{\mathrm{3}} {x}=\mathrm{4sin}\:{x}\mathrm{cos}\:{x}\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right) \\ $$$$\mathrm{3}−\mathrm{4sin}\:^{\mathrm{2}} {x}=\mathrm{4sin}\:{x}\mathrm{cos}\:{x}+\mathrm{4cos}\:^{\mathrm{2}} {x} \\ $$$$\left({after}\:{removing}\:\mathrm{sin}\:{x}\right) \\ $$$$\mathrm{3}=\mathrm{2sin}\:\mathrm{2}{x}+\mathrm{4} \\ $$$$\mathrm{sin}\:\mathrm{2}{x}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{2}{x}=\pi+\frac{\pi}{\mathrm{6}} \\ $$$${x}=\frac{\mathrm{7}\pi}{\mathrm{12}}\:. \\ $$
Commented by niraj last updated on 04/Mar/17
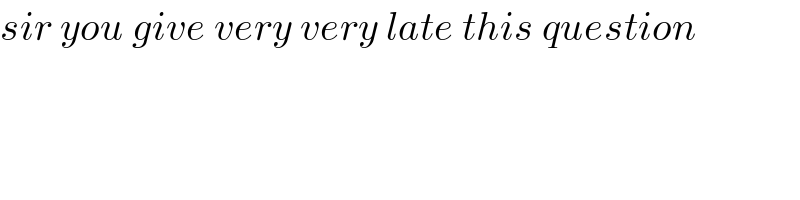
$${sir}\:{you}\:{give}\:{very}\:{very}\:{late}\:{this}\:{question} \\ $$
Commented by niraj last updated on 04/Mar/17

$$\mathrm{3}{days}\:{somthing} \\ $$
