Question Number 10033 by ridwan balatif last updated on 21/Jan/17

Answered by mrW1 last updated on 21/Jan/17
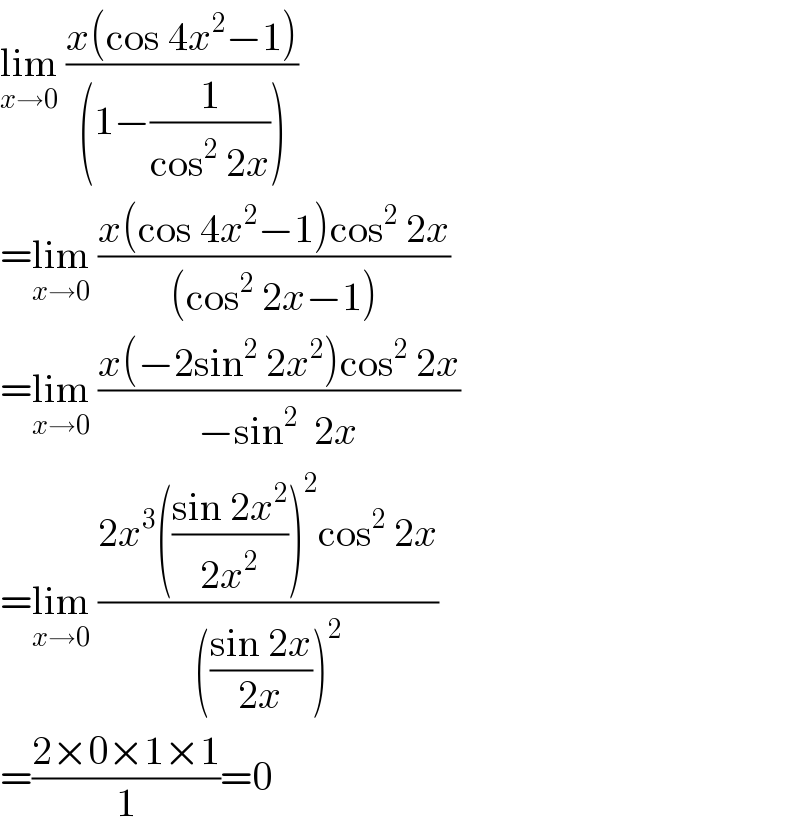
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}\left(\mathrm{cos}\:\mathrm{4}{x}^{\mathrm{2}} −\mathrm{1}\right)}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}{x}}\right)} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}\left(\mathrm{cos}\:\mathrm{4}{x}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}{x}}{\left(\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}{x}−\mathrm{1}\right)} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}\left(−\mathrm{2sin}^{\mathrm{2}} \:\mathrm{2}{x}^{\mathrm{2}} \right)\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}{x}}{−\mathrm{sin}^{\mathrm{2}} \:\:\mathrm{2}{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}{x}^{\mathrm{3}} \left(\frac{\mathrm{sin}\:\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{2}{x}^{\mathrm{2}} }\right)^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\mathrm{2}{x}}{\left(\frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{2}{x}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}×\mathrm{0}×\mathrm{1}×\mathrm{1}}{\mathrm{1}}=\mathrm{0} \\ $$
Commented by ridwan balatif last updated on 22/Jan/17

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
