Question Number 10142 by 0942679167 last updated on 26/Jan/17

Commented by prakash jain last updated on 27/Jan/17
![Σ_(i=x) ^(x+7) i^3 =Σ_(i=1) ^(x+7) i^3 −Σ_(i=1) ^(x−1) i^3 =((((x+7)(x+8))/2))^2 −((((x−1)x)/2))^2 =(1/4)[(x+7)(x+8)−x(x−1)][(x+7)(x+8)+(x−1)x] =(1/4)[16x+56][2x^2 +14x+56] =(1/4)8(2x+7)2(x^2 +7x+28) =4(2x+7)(x^2 +7x+28) y^3 =4(2x+7)(x^2 +7x+28) y=((4(2x+7)(x^2 +7x+28)))^(1/3)](https://www.tinkutara.com/question/Q10145.png)
$$\underset{{i}={x}} {\overset{{x}+\mathrm{7}} {\sum}}{i}^{\mathrm{3}} =\underset{{i}=\mathrm{1}} {\overset{{x}+\mathrm{7}} {\sum}}{i}^{\mathrm{3}} −\underset{{i}=\mathrm{1}} {\overset{{x}−\mathrm{1}} {\sum}}{i}^{\mathrm{3}} \\ $$$$=\left(\frac{\left({x}+\mathrm{7}\right)\left({x}+\mathrm{8}\right)}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\left({x}−\mathrm{1}\right){x}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left[\left({x}+\mathrm{7}\right)\left({x}+\mathrm{8}\right)−{x}\left({x}−\mathrm{1}\right)\right]\left[\left({x}+\mathrm{7}\right)\left({x}+\mathrm{8}\right)+\left({x}−\mathrm{1}\right){x}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{16}{x}+\mathrm{56}\right]\left[\mathrm{2}{x}^{\mathrm{2}} +\mathrm{14}{x}+\mathrm{56}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{8}\left(\mathrm{2}{x}+\mathrm{7}\right)\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{7}{x}+\mathrm{28}\right) \\ $$$$=\mathrm{4}\left(\mathrm{2}{x}+\mathrm{7}\right)\left({x}^{\mathrm{2}} +\mathrm{7}{x}+\mathrm{28}\right) \\ $$$${y}^{\mathrm{3}} =\mathrm{4}\left(\mathrm{2}{x}+\mathrm{7}\right)\left({x}^{\mathrm{2}} +\mathrm{7}{x}+\mathrm{28}\right) \\ $$$${y}=\sqrt[{\mathrm{3}}]{\mathrm{4}\left(\mathrm{2}{x}+\mathrm{7}\right)\left({x}^{\mathrm{2}} +\mathrm{7}{x}+\mathrm{28}\right)} \\ $$
Commented by prakash jain last updated on 27/Jan/17
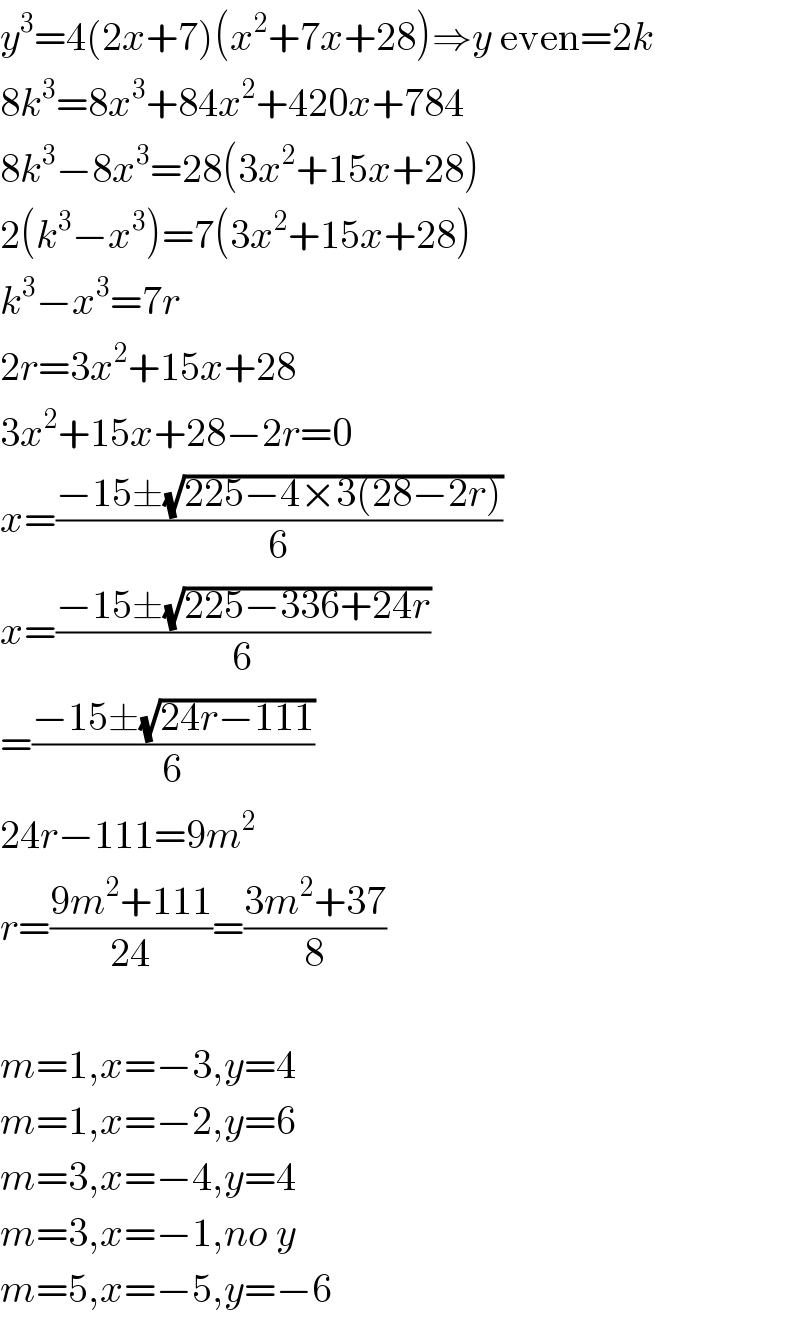
$${y}^{\mathrm{3}} =\mathrm{4}\left(\mathrm{2}{x}+\mathrm{7}\right)\left({x}^{\mathrm{2}} +\mathrm{7}{x}+\mathrm{28}\right)\Rightarrow{y}\:\mathrm{even}=\mathrm{2}{k} \\ $$$$\mathrm{8}{k}^{\mathrm{3}} =\mathrm{8}{x}^{\mathrm{3}} +\mathrm{84}{x}^{\mathrm{2}} +\mathrm{420}{x}+\mathrm{784} \\ $$$$\mathrm{8}{k}^{\mathrm{3}} −\mathrm{8}{x}^{\mathrm{3}} =\mathrm{28}\left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{15}{x}+\mathrm{28}\right) \\ $$$$\mathrm{2}\left({k}^{\mathrm{3}} −{x}^{\mathrm{3}} \right)=\mathrm{7}\left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{15}{x}+\mathrm{28}\right) \\ $$$${k}^{\mathrm{3}} −{x}^{\mathrm{3}} =\mathrm{7}{r} \\ $$$$\mathrm{2}{r}=\mathrm{3}{x}^{\mathrm{2}} +\mathrm{15}{x}+\mathrm{28} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} +\mathrm{15}{x}+\mathrm{28}−\mathrm{2}{r}=\mathrm{0} \\ $$$${x}=\frac{−\mathrm{15}\pm\sqrt{\mathrm{225}−\mathrm{4}×\mathrm{3}\left(\mathrm{28}−\mathrm{2}{r}\right)}}{\mathrm{6}} \\ $$$${x}=\frac{−\mathrm{15}\pm\sqrt{\mathrm{225}−\mathrm{336}+\mathrm{24}{r}}}{\mathrm{6}} \\ $$$$=\frac{−\mathrm{15}\pm\sqrt{\mathrm{24}{r}−\mathrm{111}}}{\mathrm{6}} \\ $$$$\mathrm{24}{r}−\mathrm{111}=\mathrm{9}{m}^{\mathrm{2}} \\ $$$${r}=\frac{\mathrm{9}{m}^{\mathrm{2}} +\mathrm{111}}{\mathrm{24}}=\frac{\mathrm{3}{m}^{\mathrm{2}} +\mathrm{37}}{\mathrm{8}} \\ $$$$ \\ $$$${m}=\mathrm{1},{x}=−\mathrm{3},{y}=\mathrm{4} \\ $$$${m}=\mathrm{1},{x}=−\mathrm{2},{y}=\mathrm{6} \\ $$$${m}=\mathrm{3},{x}=−\mathrm{4},{y}=\mathrm{4} \\ $$$${m}=\mathrm{3},{x}=−\mathrm{1},{no}\:{y} \\ $$$${m}=\mathrm{5},{x}=−\mathrm{5},{y}=−\mathrm{6} \\ $$
Commented by mrW1 last updated on 27/Jan/17

$${great}! \\ $$
