Question Number 10166 by Joel575 last updated on 28/Jan/17

Commented by Joel575 last updated on 28/Jan/17

$$\mathrm{Two}\:\mathrm{circles}\:\mathrm{with}\:\mathrm{same}\:\mathrm{center}\:\mathrm{point}\:\mathrm{have} \\ $$$$\mathrm{R}_{\mathrm{1}} \:\mathrm{and}\:\mathrm{R}_{\mathrm{2}} \:\mathrm{with}\:\mathrm{R}_{\mathrm{1}} \:<\:\mathrm{R}_{\mathrm{2}} \\ $$$$\mathrm{If}\:\mathrm{the}\:\mathrm{long}\:\mathrm{of}\:\mathrm{AB}\:\mathrm{bowstring}\:\mathrm{is}\:\mathrm{10}\:\mathrm{cm}, \\ $$$$\mathrm{count}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{blue}\:\mathrm{shade} \\ $$
Answered by mrW1 last updated on 28/Jan/17
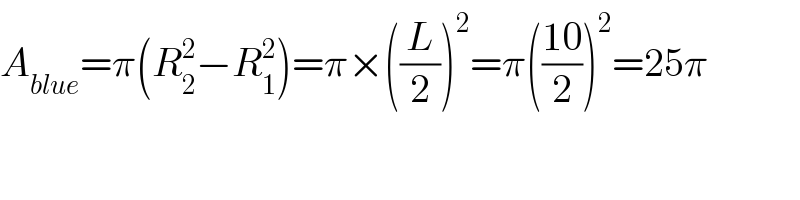
$${A}_{{blue}} =\pi\left({R}_{\mathrm{2}} ^{\mathrm{2}} −{R}_{\mathrm{1}} ^{\mathrm{2}} \right)=\pi×\left(\frac{{L}}{\mathrm{2}}\right)^{\mathrm{2}} =\pi\left(\frac{\mathrm{10}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{25}\pi \\ $$
