Question Number 10188 by ridwan balatif last updated on 29/Jan/17

Commented by ridwan balatif last updated on 29/Jan/17
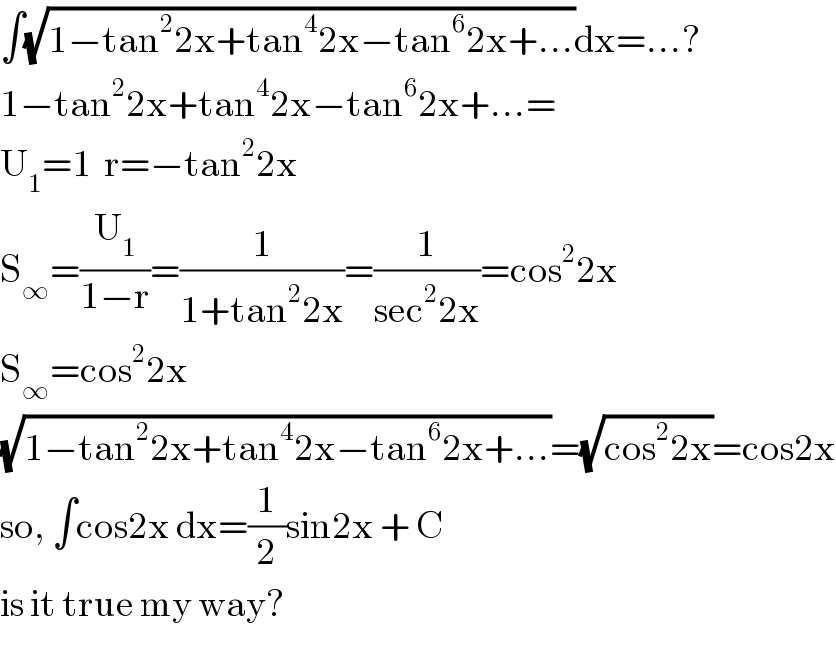
$$\int\sqrt{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{2x}+\mathrm{tan}^{\mathrm{4}} \mathrm{2x}−\mathrm{tan}^{\mathrm{6}} \mathrm{2x}+…}\mathrm{dx}=…? \\ $$$$\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{2x}+\mathrm{tan}^{\mathrm{4}} \mathrm{2x}−\mathrm{tan}^{\mathrm{6}} \mathrm{2x}+…=\: \\ $$$$\mathrm{U}_{\mathrm{1}} =\mathrm{1}\:\:\mathrm{r}=−\mathrm{tan}^{\mathrm{2}} \mathrm{2x} \\ $$$$\mathrm{S}_{\infty} =\frac{\mathrm{U}_{\mathrm{1}} }{\mathrm{1}−\mathrm{r}}=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{2x}}=\frac{\mathrm{1}}{\mathrm{sec}^{\mathrm{2}} \mathrm{2x}}=\mathrm{cos}^{\mathrm{2}} \mathrm{2x} \\ $$$$\mathrm{S}_{\infty} =\mathrm{cos}^{\mathrm{2}} \mathrm{2x} \\ $$$$\sqrt{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{2x}+\mathrm{tan}^{\mathrm{4}} \mathrm{2x}−\mathrm{tan}^{\mathrm{6}} \mathrm{2x}+…}=\sqrt{\mathrm{cos}^{\mathrm{2}} \mathrm{2x}}=\mathrm{cos2x} \\ $$$$\mathrm{so},\:\int\mathrm{cos2x}\:\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin2x}\:+\:\mathrm{C} \\ $$$$\mathrm{is}\:\mathrm{it}\:\mathrm{true}\:\mathrm{my}\:\mathrm{way}? \\ $$
