Question Number 10268 by j.masanja06@gmail.com last updated on 01/Feb/17
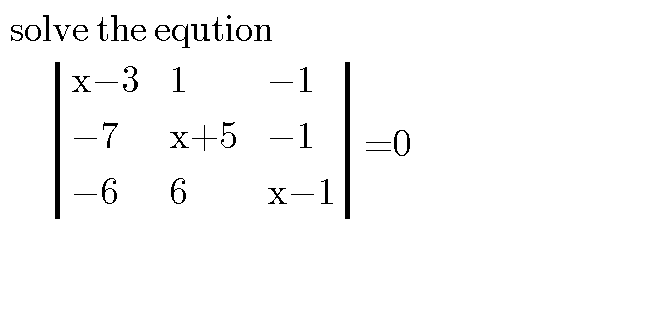
Answered by sandy_suhendra last updated on 01/Feb/17
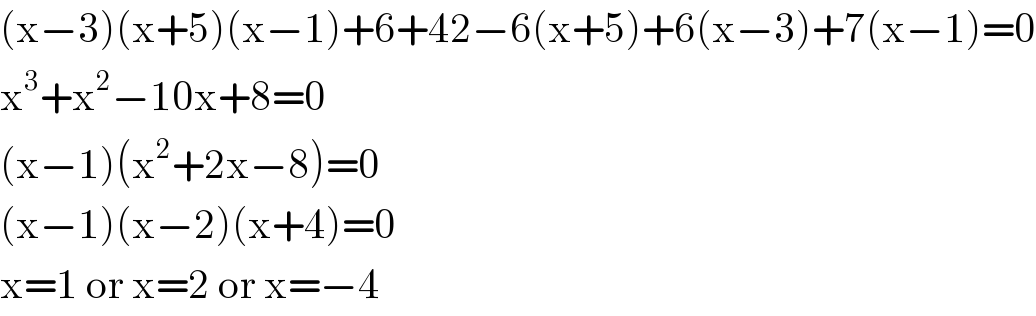
$$\left(\mathrm{x}−\mathrm{3}\right)\left(\mathrm{x}+\mathrm{5}\right)\left(\mathrm{x}−\mathrm{1}\right)+\mathrm{6}+\mathrm{42}−\mathrm{6}\left(\mathrm{x}+\mathrm{5}\right)+\mathrm{6}\left(\mathrm{x}−\mathrm{3}\right)+\mathrm{7}\left(\mathrm{x}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} −\mathrm{10x}+\mathrm{8}=\mathrm{0} \\ $$$$\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{8}\right)=\mathrm{0} \\ $$$$\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}+\mathrm{4}\right)=\mathrm{0} \\ $$$$\mathrm{x}=\mathrm{1}\:\mathrm{or}\:\mathrm{x}=\mathrm{2}\:\mathrm{or}\:\mathrm{x}=−\mathrm{4} \\ $$
Answered by arge last updated on 04/Feb/17

$${x}−\mathrm{3}\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:−\mathrm{1} \\ $$$$ \\ $$$$−\mathrm{7}\:\:\:\:\:{x}+\mathrm{5}\:\:\:\:−\mathrm{1}\: \\ $$$$ \\ $$$$−\mathrm{6}\:\:\:\:\:\:\:\:\mathrm{6}\:\:\:\:\:{x}−\mathrm{1} \\ $$$$ \\ $$$${x}−\mathrm{3}\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:−\mathrm{1} \\ $$$$ \\ $$$$−\mathrm{7}\:\:\:\:\:{x}+\mathrm{5}\:\:\:\:\:−\mathrm{1} \\ $$$$ \\ $$$$ \\ $$$$\left({x}−\mathrm{3}\right)\left({x}+\mathrm{5}\right)\left({x}−\mathrm{1}\right)+\left(−\mathrm{7}×\mathrm{6}×−\mathrm{1}\right)+\left(−\mathrm{6}×\mathrm{1}×−\mathrm{1}\right)−\left\{−\mathrm{1}\left({x}+\mathrm{5}\right)\left(−\mathrm{6}\right)+\left[−\mathrm{1}\left(\mathrm{6}\right)\left({x}−\mathrm{3}\right)+\left({x}−\mathrm{1}\right)\left(\mathrm{1}\right)\left(−\mathrm{7}\right)\right\}=\mathrm{0}\right. \\ $$$${x}^{\mathrm{3}} +{x}^{\mathrm{2}} −\mathrm{24}{x}+\mathrm{22}=\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{22}\right)=\mathrm{0} \\ $$$$ \\ $$$${x}=\mathrm{1} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
