Menu Close

Question-10381

Tinku Tara 0 Comments
Pin




Question Number 10381 by ridwan balatif last updated on 06/Feb/17
Commented by ridwan balatif last updated on 06/Feb/17
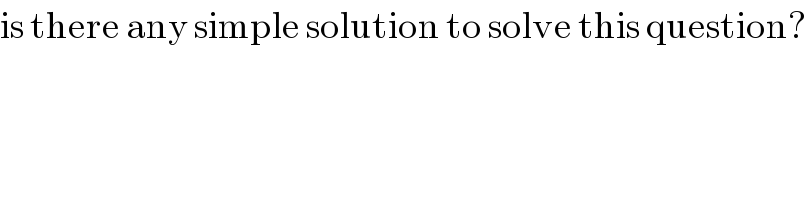
is there any simple solution to solve this question?
$$\mathrm{is}\:\mathrm{there}\:\mathrm{any}\:\mathrm{simple}\:\mathrm{solution}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{question}? \\ $$
Answered by mrW1 last updated on 06/Feb/17
let t=x^(1/6) ⇒x=t^6 x^(1/3) =t^2 x^(1/2) =t^3 x^(2/3) =t^4 x^(4/3) =t^8 (((x^(1/3) −x^(1/6) )(x^(1/2) +x)(x^(1/2) +x^(1/3) +x^(2/3) ))/((x^(4/3) −x)(x+x^(1/3) +x^(2/3) ))) =(((t^2 −t)(t^3 +t^6 )(t^3 +t^2 +t^4 ))/((t^8 −t^6 )(t^6 +t^2 +t^4 ))) =(((t−1)(1+t^3 )(t+1+t^2 )t^6 )/((t^2 −1)(t^4 +1+t^2 )t^8 )) =(((t^3 +1)(t^2 +t+1))/((t+1)(t^4 +t^2 +1)t^2 )) =(((t+1)(t^2 −t+1)(t^2 +t+1))/((t+1)(t^4 +t^2 +1)t^2 )) =((t^4 +t^2 +1)/((t^4 +t^2 +1)t^2 )) =(1/t^2 )=(1/x^(1/3) )=x^(−(1/3)) ⇒ answer (A)
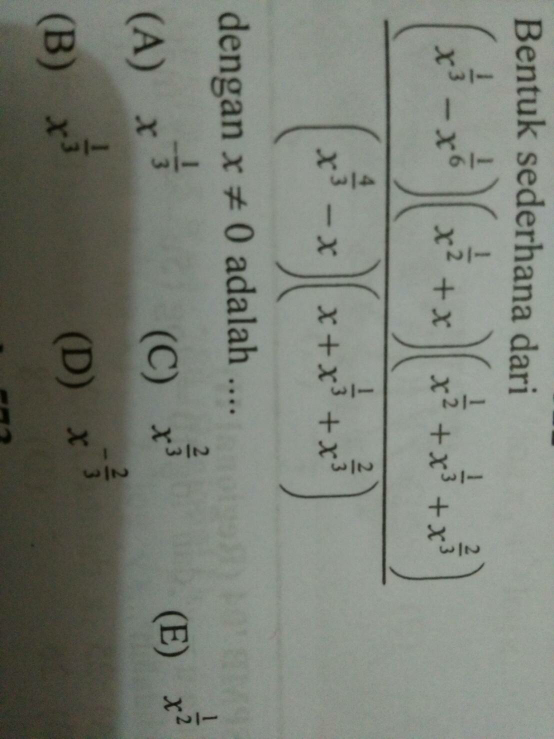
$${let}\:{t}={x}^{\frac{\mathrm{1}}{\mathrm{6}}} \\ $$$$\Rightarrow{x}={t}^{\mathrm{6}} \\ $$$${x}^{\frac{\mathrm{1}}{\mathrm{3}}} ={t}^{\mathrm{2}} \\ $$$${x}^{\frac{\mathrm{1}}{\mathrm{2}}} ={t}^{\mathrm{3}} \\ $$$${x}^{\frac{\mathrm{2}}{\mathrm{3}}} ={t}^{\mathrm{4}} \\ $$$${x}^{\frac{\mathrm{4}}{\mathrm{3}}} ={t}^{\mathrm{8}} \\ $$$$ \\ $$$$\frac{\left({x}^{\frac{\mathrm{1}}{\mathrm{3}}} −{x}^{\frac{\mathrm{1}}{\mathrm{6}}} \right)\left({x}^{\frac{\mathrm{1}}{\mathrm{2}}} +{x}\right)\left({x}^{\frac{\mathrm{1}}{\mathrm{2}}} +{x}^{\frac{\mathrm{1}}{\mathrm{3}}} +{x}^{\frac{\mathrm{2}}{\mathrm{3}}} \right)}{\left({x}^{\frac{\mathrm{4}}{\mathrm{3}}} −{x}\right)\left({x}+{x}^{\frac{\mathrm{1}}{\mathrm{3}}} +{x}^{\frac{\mathrm{2}}{\mathrm{3}}} \right)} \\ $$$$=\frac{\left({t}^{\mathrm{2}} −{t}\right)\left({t}^{\mathrm{3}} +{t}^{\mathrm{6}} \right)\left({t}^{\mathrm{3}} +{t}^{\mathrm{2}} +{t}^{\mathrm{4}} \right)}{\left({t}^{\mathrm{8}} −{t}^{\mathrm{6}} \right)\left({t}^{\mathrm{6}} +{t}^{\mathrm{2}} +{t}^{\mathrm{4}} \right)} \\ $$$$=\frac{\left({t}−\mathrm{1}\right)\left(\mathrm{1}+{t}^{\mathrm{3}} \right)\left({t}+\mathrm{1}+{t}^{\mathrm{2}} \right){t}^{\mathrm{6}} }{\left({t}^{\mathrm{2}} −\mathrm{1}\right)\left({t}^{\mathrm{4}} +\mathrm{1}+{t}^{\mathrm{2}} \right){t}^{\mathrm{8}} } \\ $$$$=\frac{\left({t}^{\mathrm{3}} +\mathrm{1}\right)\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)}{\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\mathrm{1}\right){t}^{\mathrm{2}} } \\ $$$$=\frac{\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)}{\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\mathrm{1}\right){t}^{\mathrm{2}} } \\ $$$$=\frac{{t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\mathrm{1}}{\left({t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\mathrm{1}\right){t}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{{t}^{\mathrm{2}} }=\frac{\mathrm{1}}{{x}^{\frac{\mathrm{1}}{\mathrm{3}}} }={x}^{−\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$ \\ $$$$\Rightarrow\:{answer}\:\left({A}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *