Question Number 10408 by konen last updated on 07/Feb/17

Answered by mrW1 last updated on 08/Feb/17
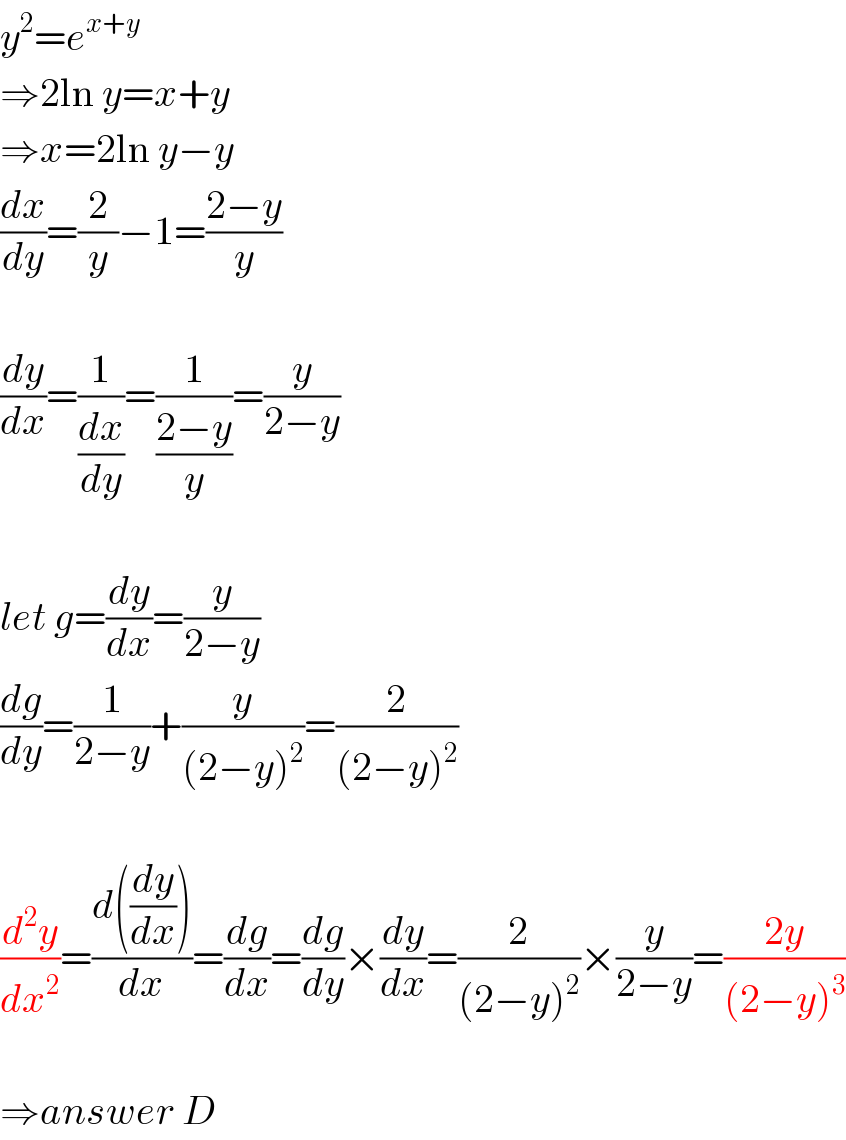
$${y}^{\mathrm{2}} ={e}^{{x}+{y}} \\ $$$$\Rightarrow\mathrm{2ln}\:{y}={x}+{y} \\ $$$$\Rightarrow{x}=\mathrm{2ln}\:{y}−{y} \\ $$$$\frac{{dx}}{{dy}}=\frac{\mathrm{2}}{{y}}−\mathrm{1}=\frac{\mathrm{2}−{y}}{{y}} \\ $$$$ \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{1}}{\frac{{dx}}{{dy}}}=\frac{\mathrm{1}}{\frac{\mathrm{2}−{y}}{{y}}}=\frac{{y}}{\mathrm{2}−{y}} \\ $$$$ \\ $$$${let}\:{g}=\frac{{dy}}{{dx}}=\frac{{y}}{\mathrm{2}−{y}} \\ $$$$\frac{{dg}}{{dy}}=\frac{\mathrm{1}}{\mathrm{2}−{y}}+\frac{{y}}{\left(\mathrm{2}−{y}\right)^{\mathrm{2}} }=\frac{\mathrm{2}}{\left(\mathrm{2}−{y}\right)^{\mathrm{2}} } \\ $$$$ \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{{d}\left(\frac{{dy}}{{dx}}\right)}{{dx}}=\frac{{dg}}{{dx}}=\frac{{dg}}{{dy}}×\frac{{dy}}{{dx}}=\frac{\mathrm{2}}{\left(\mathrm{2}−{y}\right)^{\mathrm{2}} }×\frac{{y}}{\mathrm{2}−{y}}=\frac{\mathrm{2}{y}}{\left(\mathrm{2}−{y}\right)^{\mathrm{3}} } \\ $$$$ \\ $$$$\Rightarrow{answer}\:{D} \\ $$
