Question Number 10435 by Joel575 last updated on 09/Feb/17

Commented by Joel575 last updated on 09/Feb/17

$$\mathrm{The}\:\mathrm{side}\:\mathrm{length}\:\mathrm{of}\:\mathrm{the}\:\mathrm{square}\:\mathrm{is}\:\mathrm{1}\:\mathrm{cm}. \\ $$$$\mathrm{5}\:\mathrm{circles}\:\mathrm{have}\:\mathrm{same}\:\mathrm{radius}. \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}'\mathrm{s}\:\mathrm{radius}? \\ $$
Answered by sandy_suhendra last updated on 09/Feb/17
Commented by sandy_suhendra last updated on 09/Feb/17

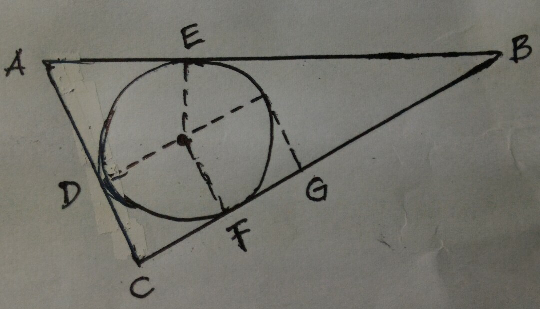
$$\mathrm{let}\:\mathrm{AC}=\mathrm{GB}=\mathrm{x}\:\mathrm{and}\:\mathrm{CD}=\mathrm{CF}=\mathrm{FG}=\mathrm{r}\:\: \\ $$$$\mathrm{so}\:\mathrm{AD}=\mathrm{AE}=\mathrm{x}−\mathrm{r} \\ $$$$\:\:\:\:\:\:\mathrm{FB}=\mathrm{EB}=\mathrm{x}+\mathrm{r} \\ $$$$\mathrm{AE}+\mathrm{EB}=\mathrm{1} \\ $$$$\mathrm{x}−\mathrm{r}+\mathrm{x}+\mathrm{r}=\mathrm{1}\:\Rightarrow\:\mathrm{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{AC}=\mathrm{x}=\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{and}\:\mathrm{CB}=\mathrm{2r}+\mathrm{x}=\mathrm{2r}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{Phytagoras}\:\mathrm{theorem}\:: \\ $$$$\mathrm{AC}^{\mathrm{2}} +\mathrm{CB}^{\mathrm{2}} =\mathrm{AB}^{\mathrm{2}} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\mathrm{2r}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{1}^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{4r}^{\mathrm{2}} +\mathrm{2r}+\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{1} \\ $$$$\mathrm{4r}^{\mathrm{2}} +\mathrm{2r}−\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0} \\ $$$$\mathrm{8r}^{\mathrm{2}} +\mathrm{4r}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{r}\:=\:\frac{−\mathrm{4}\pm\sqrt{\mathrm{16}+\mathrm{32}}}{\mathrm{16}} \\ $$$$\mathrm{r}\:=\:\frac{−\mathrm{4}+\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{16}}\:=\:\frac{−\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$$$\left(\mathrm{r}\:\mathrm{must}\:\mathrm{be}\:\mathrm{positive}\right) \\ $$
