Question Number 10510 by ajfour last updated on 15/Feb/17

Answered by mrW1 last updated on 15/Feb/17
![2sin x+3cos x =(√(13))×((2/( (√(13))))sin x+(3/( (√(13))))cos x) =(√(13))×(sin xcos t+cos xsin t) =(√(13))×sin (x+t) with t=sin^(−1) ((3/( (√(13))))) and tan t=(3/2) ∫(1/((2sin x+3cos x)^2 ))dx =∫(1/(13sin^2 (x+t)))dx =(1/(13))×∫(1/(sin^2 (x+t)))d(x+t) =(1/(13))×[−cot (x+t)]+C =(1/(13))×(−((1−tan x tan t)/(tan x+tan t)))+C =(1/(13))×((−1+(3/2)tan x)/(tan x+(3/2)))+C =(1/(13))×((3tan x−2)/(2tan x+3))+C =(1/(13))×((3sin x−2cos x)/(2sin x+3cos x))+C](https://www.tinkutara.com/question/Q10511.png)
$$\mathrm{2sin}\:{x}+\mathrm{3cos}\:{x} \\ $$$$=\sqrt{\mathrm{13}}×\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{13}}}\mathrm{sin}\:{x}+\frac{\mathrm{3}}{\:\sqrt{\mathrm{13}}}\mathrm{cos}\:{x}\right) \\ $$$$=\sqrt{\mathrm{13}}×\left(\mathrm{sin}\:{x}\mathrm{cos}\:{t}+\mathrm{cos}\:{x}\mathrm{sin}\:{t}\right) \\ $$$$=\sqrt{\mathrm{13}}×\mathrm{sin}\:\left({x}+{t}\right) \\ $$$${with}\:{t}=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{13}}}\right)\:{and}\:\mathrm{tan}\:{t}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$ \\ $$$$\int\frac{\mathrm{1}}{\left(\mathrm{2sin}\:{x}+\mathrm{3cos}\:{x}\right)^{\mathrm{2}} }{dx} \\ $$$$=\int\frac{\mathrm{1}}{\mathrm{13sin}^{\mathrm{2}} \:\left({x}+{t}\right)}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{13}}×\int\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \:\left({x}+{t}\right)}{d}\left({x}+{t}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{13}}×\left[−\mathrm{cot}\:\left({x}+{t}\right)\right]+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{13}}×\left(−\frac{\mathrm{1}−\mathrm{tan}\:{x}\:\mathrm{tan}\:{t}}{\mathrm{tan}\:{x}+\mathrm{tan}\:{t}}\right)+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{13}}×\frac{−\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{tan}\:{x}}{\mathrm{tan}\:{x}+\frac{\mathrm{3}}{\mathrm{2}}}+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{13}}×\frac{\mathrm{3tan}\:{x}−\mathrm{2}}{\mathrm{2tan}\:{x}+\mathrm{3}}+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{13}}×\frac{\mathrm{3sin}\:{x}−\mathrm{2cos}\:{x}}{\mathrm{2sin}\:{x}+\mathrm{3cos}\:{x}}+{C} \\ $$
Answered by robocop last updated on 15/Feb/17
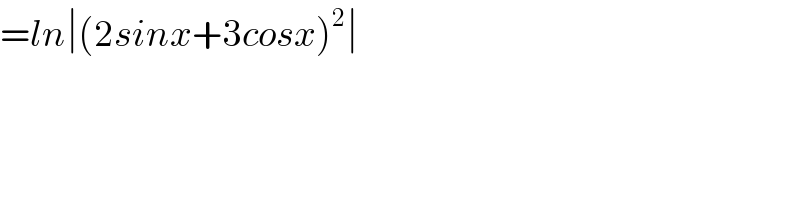
$$={ln}\mid\left(\mathrm{2}{sinx}+\mathrm{3}{cosx}\right)^{\mathrm{2}} \mid \\ $$$$ \\ $$
