Question Number 10566 by krist last updated on 18/Feb/17
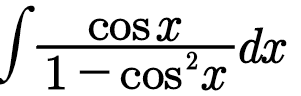
Answered by ridwan balatif last updated on 18/Feb/17

$$\int\frac{\mathrm{cos}{x}}{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} {x}}{dx} \\ $$$$=\int\frac{\mathrm{cos}{x}}{\mathrm{sin}^{\mathrm{2}} {x}}{dx} \\ $$$$=\int\frac{\mathrm{cos}{x}}{\mathrm{sin}{x}}×\frac{\mathrm{1}}{\mathrm{sin}{x}}{dx} \\ $$$$=\int\mathrm{cotan}{x}×\mathrm{cosec}{xdx} \\ $$$$=−\mathrm{cosec}{x}+\mathrm{C} \\ $$
Answered by mrW1 last updated on 18/Feb/17
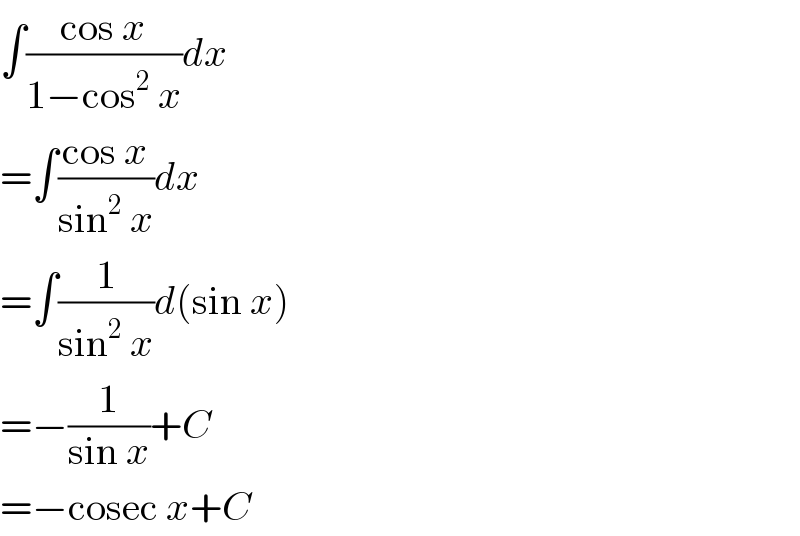
$$\int\frac{\mathrm{cos}\:{x}}{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:{x}}{dx} \\ $$$$=\int\frac{\mathrm{cos}\:{x}}{\mathrm{sin}^{\mathrm{2}} \:{x}}{dx} \\ $$$$=\int\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \:{x}}{d}\left(\mathrm{sin}\:{x}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{sin}\:{x}}+{C} \\ $$$$=−\mathrm{cosec}\:{x}+{C} \\ $$
