Question-10621

Question Number 10621 by ketto last updated on 20/Feb/17

Answered by mrW1 last updated on 20/Feb/17

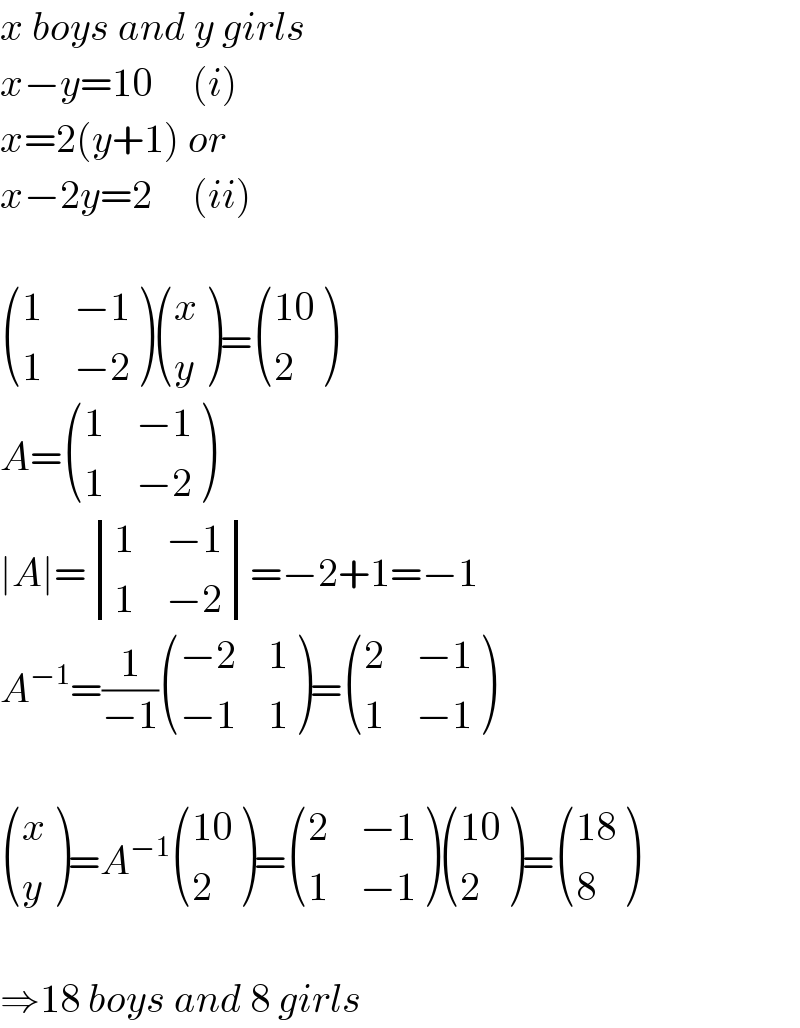
x b o y s a n d y g i r l s

x - y = 10 (i)

x = 2 (y + 1) o r

x - 2 y = 2 (i i)

(\begin{matrix} 1 & - 1 \\ 1 & - 2 \end{matrix}) (\begin{matrix} x \\ y \end{matrix}) = (\begin{matrix} 10 \\ 2 \end{matrix})

A = (\begin{matrix} 1 & - 1 \\ 1 & - 2 \end{matrix})

∣ A ∣= | \begin{matrix} 1 & - 1 \\ 1 & - 2 \end{matrix} | = - 2 + 1 = - 1

A^{- 1} = \frac{1}{- 1} (\begin{matrix} - 2 & 1 \\ - 1 & 1 \end{matrix}) = (\begin{matrix} 2 & - 1 \\ 1 & - 1 \end{matrix})

(\begin{matrix} x \\ y \end{matrix}) = A^{- 1} (\begin{matrix} 10 \\ 2 \end{matrix}) = (\begin{matrix} 2 & - 1 \\ 1 & - 1 \end{matrix}) (\begin{matrix} 10 \\ 2 \end{matrix}) = (\begin{matrix} 18 \\ 8 \end{matrix})

\Rightarrow 18 b o y s a n d 8 g i r l s

Facebook Tweet Pin