Question Number 10820 by chux last updated on 26/Feb/17
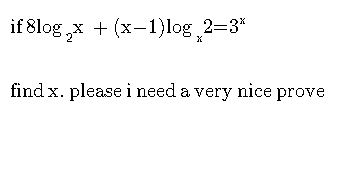
Answered by bar Jesús last updated on 26/Feb/17
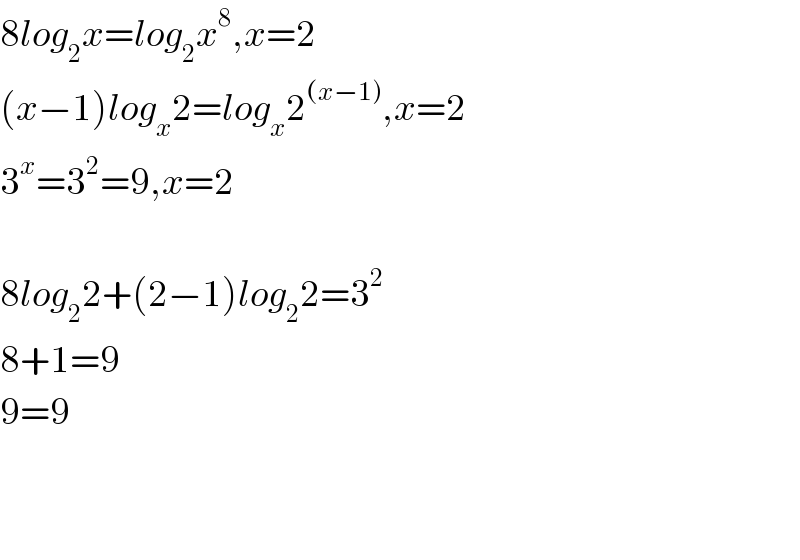
$$\mathrm{8}{log}_{\mathrm{2}} {x}={log}_{\mathrm{2}} {x}^{\mathrm{8}} ,{x}=\mathrm{2} \\ $$$$\left({x}−\mathrm{1}\right){log}_{{x}} \mathrm{2}={log}_{{x}} \mathrm{2}^{\left({x}−\mathrm{1}\right)} ,{x}=\mathrm{2} \\ $$$$\mathrm{3}^{{x}} =\mathrm{3}^{\mathrm{2}} =\mathrm{9},{x}=\mathrm{2} \\ $$$$ \\ $$$$\mathrm{8}{log}_{\mathrm{2}} \mathrm{2}+\left(\mathrm{2}−\mathrm{1}\right){log}_{\mathrm{2}} \mathrm{2}=\mathrm{3}^{\mathrm{2}} \\ $$$$\mathrm{8}+\mathrm{1}=\mathrm{9} \\ $$$$\mathrm{9}=\mathrm{9} \\ $$$$ \\ $$$$ \\ $$
Commented by mrW1 last updated on 27/Feb/17

$${and}\:{x}\approx\mathrm{1}.\mathrm{3855} \\ $$
