Question Number 10981 by ridwan balatif last updated on 05/Mar/17

Commented by prakash jain last updated on 06/Mar/17
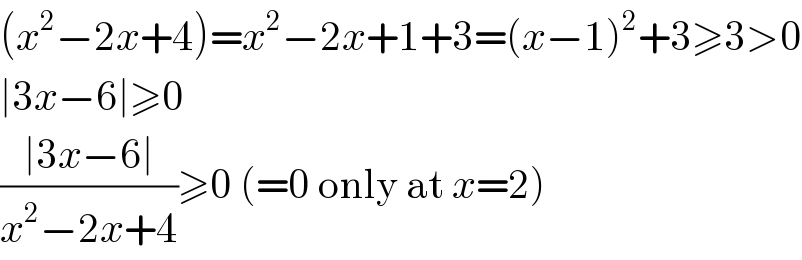
$$\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{4}\right)={x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}+\mathrm{3}=\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}\geqslant\mathrm{3}>\mathrm{0} \\ $$$$\mid\mathrm{3}{x}−\mathrm{6}\mid\geqslant\mathrm{0} \\ $$$$\frac{\mid\mathrm{3}{x}−\mathrm{6}\mid}{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{4}}\geqslant\mathrm{0}\:\left(=\mathrm{0}\:\mathrm{only}\:\mathrm{at}\:{x}=\mathrm{2}\right) \\ $$
Answered by Mechas88 last updated on 05/Mar/17
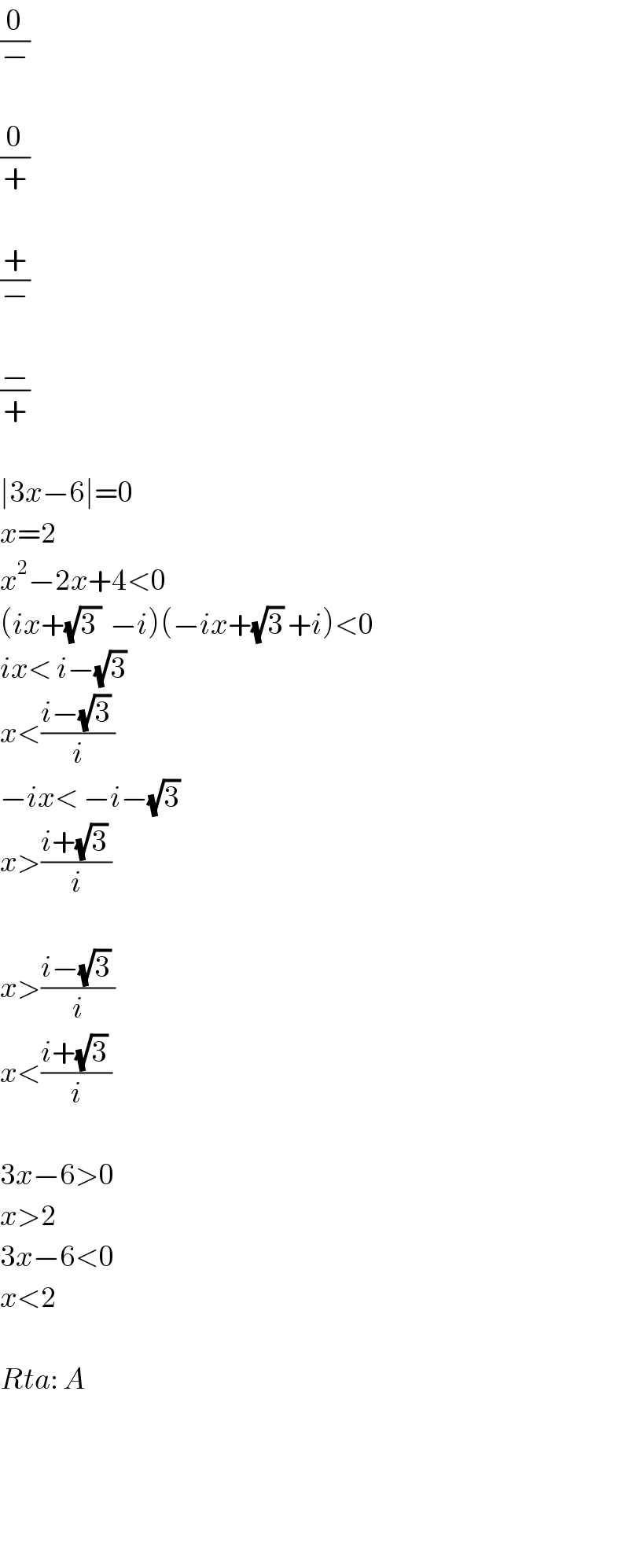
$$\frac{\mathrm{0}}{−} \\ $$$$ \\ $$$$\frac{\mathrm{0}}{+} \\ $$$$ \\ $$$$\frac{+}{−} \\ $$$$ \\ $$$$\frac{−}{+} \\ $$$$ \\ $$$$\mid\mathrm{3}{x}−\mathrm{6}\mid=\mathrm{0} \\ $$$${x}=\mathrm{2} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{4}<\mathrm{0} \\ $$$$\left({ix}+\sqrt{\mathrm{3}\:}\:\:−{i}\right)\left(−{ix}+\sqrt{\mathrm{3}}\:+{i}\right)<\mathrm{0} \\ $$$${ix}<\:{i}−\sqrt{\mathrm{3}}\: \\ $$$${x}<\frac{{i}−\sqrt{\mathrm{3}}\:}{{i}} \\ $$$$−{ix}<\:−{i}−\sqrt{\mathrm{3}}\: \\ $$$${x}>\frac{{i}+\sqrt{\mathrm{3}}\:}{{i}} \\ $$$$ \\ $$$${x}>\frac{{i}−\sqrt{\mathrm{3}}\:}{{i}} \\ $$$${x}<\frac{{i}+\sqrt{\mathrm{3}}\:}{{i}} \\ $$$$ \\ $$$$\mathrm{3}{x}−\mathrm{6}>\mathrm{0} \\ $$$${x}>\mathrm{2} \\ $$$$\mathrm{3}{x}−\mathrm{6}<\mathrm{0} \\ $$$${x}<\mathrm{2} \\ $$$$ \\ $$$${Rta}:\:{A} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by prakash jain last updated on 06/Mar/17
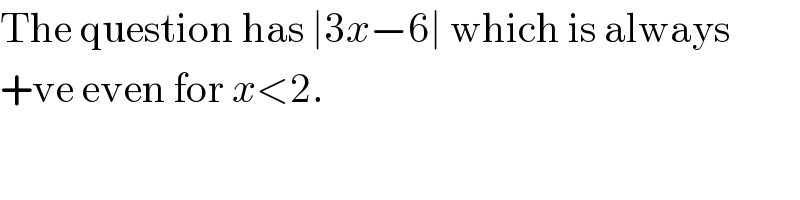
$$\mathrm{The}\:\mathrm{question}\:\mathrm{has}\:\mid\mathrm{3}{x}−\mathrm{6}\mid\:\mathrm{which}\:\mathrm{is}\:\mathrm{always} \\ $$$$+\mathrm{ve}\:\mathrm{even}\:\mathrm{for}\:{x}<\mathrm{2}. \\ $$
