Question Number 11019 by ridwan balatif last updated on 07/Mar/17
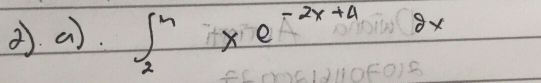
Answered by bahmanfeshki last updated on 07/Mar/17
![I=∫_2 ^n xe^(−2x+4) dx=−(1/2)([xe^(−2x+4) ]_2 ^n −∫_(2 ) ^n e^(−2x+4) dx)](https://www.tinkutara.com/question/Q11028.png)
$${I}=\int_{\mathrm{2}} ^{{n}} {xe}^{−\mathrm{2}{x}+\mathrm{4}} \:{dx}=−\frac{\mathrm{1}}{\mathrm{2}}\left(\left[{xe}^{−\mathrm{2}{x}+\mathrm{4}} \right]_{\mathrm{2}} ^{{n}} −\int_{\mathrm{2}\:\:} ^{{n}} {e}^{−\mathrm{2}{x}+\mathrm{4}} \:{dx}\right) \\ $$
Answered by geovane10math last updated on 07/Mar/17
![∫_2 ^n x∙e^(−2x+A) dx = F(n) − F(2) ∫x∙e^(−2x+A) dx = ∫x∙e^(−2x) ∙e^A dx = = e^A ∫x∙e^(−2x) dx −2x = u ⇒ (du/dx) = −2 ⇒ dx = − (du/2) e^A ∫− (u/2)∙e^u du = e^A ∙(1/2)∙∫u∙e^u du = = (e^A /2)∫u∙e^u du ∫u∙e^u du u = s , e^u du = dt ∫s dt = st − ∫t ds ∫u∙e^u du = u(e^u + c_1 ) − ∫[e^u + c_1 ]du ∫u∙e^u du = ue^u + c_1 u − (e^u + c_1 u + C) ∫ue^u du = ue^u + c_1 u − e^u − c_1 u − C ∫ue^u du = e^u (u − 1) − C (e^A /2)[e^u (u − 1) − C] = (e^A /2)[e^(−2x) (−2x − 1 − C)] ∫x∙e^(−2x+A) dx = − (e^A /2)[e^(−2x) (2x +1 + C)] F(n) − F(2) = = − (e^A /2)[e^(−2n) (2n + 1 + C)] − (− (e^A /2)[(5 + C)]) = − (e^A /2)[e^(−2n) ( 2n + 1 + C)] + (e^A /2)(5 + C)](https://www.tinkutara.com/question/Q11029.png)
$$\int_{\mathrm{2}} ^{{n}} {x}\centerdot{e}^{−\mathrm{2}{x}+{A}} \:\mathrm{dx}\:=\:{F}\left({n}\right)\:−\:{F}\left(\mathrm{2}\right) \\ $$$$\int{x}\centerdot{e}^{−\mathrm{2}{x}+{A}} \:\mathrm{dx}\:=\:\int{x}\centerdot{e}^{−\mathrm{2}{x}} \centerdot{e}^{{A}} \:\mathrm{dx}\:=\: \\ $$$$=\:{e}^{{A}} \int{x}\centerdot{e}^{−\mathrm{2}{x}} \:\mathrm{dx}\: \\ $$$$−\mathrm{2}{x}\:=\:{u}\:\Rightarrow\:\frac{{du}}{{dx}}\:=\:−\mathrm{2}\:\Rightarrow\:{dx}\:=\:−\:\frac{{du}}{\mathrm{2}} \\ $$$${e}^{{A}} \int−\:\frac{{u}}{\mathrm{2}}\centerdot{e}^{{u}} \:\mathrm{du}\:=\:{e}^{{A}} \centerdot\frac{\mathrm{1}}{\mathrm{2}}\centerdot\int{u}\centerdot{e}^{{u}} \:\mathrm{du}\:=\: \\ $$$$=\:\frac{{e}^{{A}} }{\mathrm{2}}\int{u}\centerdot{e}^{{u}} \:\mathrm{du} \\ $$$$\int{u}\centerdot{e}^{{u}} \:\mathrm{du}\:\:\:\:\:\:\:\:\:\: \\ $$$${u}\:=\:{s}\:,\:{e}^{{u}} \:\mathrm{du}\:=\:{dt} \\ $$$$\int{s}\:\mathrm{dt}\:=\:{st}\:−\:\int{t}\:\mathrm{ds} \\ $$$$\int{u}\centerdot{e}^{{u}} \:\mathrm{du}\:=\:{u}\left({e}^{{u}} \:+\:{c}_{\mathrm{1}} \right)\:−\:\int\left[{e}^{{u}} \:+\:{c}_{\mathrm{1}} \right]\mathrm{du} \\ $$$$\int{u}\centerdot{e}^{{u}} \:\mathrm{du}\:=\:{ue}^{{u}} \:+\:{c}_{\mathrm{1}} {u}\:−\:\left({e}^{{u}} \:+\:{c}_{\mathrm{1}} {u}\:+\:{C}\right) \\ $$$$\int{ue}^{{u}} \:\mathrm{du}\:=\:{ue}^{{u}} \:+\:{c}_{\mathrm{1}} {u}\:−\:{e}^{{u}} \:−\:{c}_{\mathrm{1}} {u}\:−\:{C} \\ $$$$\int{ue}^{{u}} \:\mathrm{du}\:=\:{e}^{{u}} \left({u}\:−\:\mathrm{1}\right)\:−\:{C} \\ $$$$\frac{{e}^{{A}} }{\mathrm{2}}\left[{e}^{{u}} \left({u}\:−\:\mathrm{1}\right)\:−\:{C}\right]\:=\:\frac{{e}^{{A}} }{\mathrm{2}}\left[{e}^{−\mathrm{2}{x}} \left(−\mathrm{2}{x}\:−\:\mathrm{1}\:−\:{C}\right)\right] \\ $$$$\int{x}\centerdot{e}^{−\mathrm{2}{x}+{A}} \:\mathrm{dx}\:=\:−\:\frac{{e}^{{A}} }{\mathrm{2}}\left[{e}^{−\mathrm{2}{x}} \left(\mathrm{2}{x}\:+\mathrm{1}\:+\:{C}\right)\right] \\ $$$${F}\left({n}\right)\:−\:{F}\left(\mathrm{2}\right)\:=\: \\ $$$$=\:−\:\frac{{e}^{{A}} }{\mathrm{2}}\left[{e}^{−\mathrm{2}{n}} \left(\mathrm{2}{n}\:+\:\mathrm{1}\:+\:{C}\right)\right]\:−\:\left(−\:\frac{{e}^{{A}} }{\mathrm{2}}\left[\left(\mathrm{5}\:+\:{C}\right)\right]\right) \\ $$$$\:=\:−\:\frac{{e}^{{A}} }{\mathrm{2}}\left[{e}^{−\mathrm{2}{n}} \left(\:\mathrm{2}{n}\:+\:\mathrm{1}\:+\:{C}\right)\right]\:+\:\frac{{e}^{{A}} }{\mathrm{2}}\left(\mathrm{5}\:+\:{C}\right) \\ $$$$ \\ $$
