Menu Close

Question-11139

Tinku Tara 0 Comments
Pin




Question Number 11139 by Joel576 last updated on 13/Mar/17
Commented by Joel576 last updated on 13/Mar/17
A real number t, so there is a three−ordered−pair solution {x, y, z} that fulfilled x^(2 ) + 2y^2 = 3z and x + y + z = t Find t Answer : t = −(9/8) 3t = 3x + 3y + 3z = 3x + 3y + x^2 + 2y^2 = (x + (3/2))^2 + 2(y + (3/4))^2 − ((27)/8) In order to have only a three−ordered−pair solution, so must be 3t = − ((27)/8) ⇔ t = − (9/8) Is there anyone who can explain that explanation above?
$$\mathrm{A}\:\mathrm{real}\:\mathrm{number}\:{t},\:\mathrm{so}\:\mathrm{there}\:\mathrm{is}\:\mathrm{a}\:\mathrm{three}−\mathrm{ordered}−\mathrm{pair} \\ $$$$\mathrm{solution}\:\left\{{x},\:{y},\:{z}\right\}\:\mathrm{that}\:\mathrm{fulfilled} \\ $$$${x}^{\mathrm{2}\:} \:+\:\mathrm{2}{y}^{\mathrm{2}} \:=\:\mathrm{3}{z}\:\:\:\mathrm{and}\:\:\:{x}\:+\:{y}\:+\:{z}\:=\:{t} \\ $$$$\mathrm{Find}\:{t} \\ $$$$ \\ $$$$\mathrm{Answer}\::\:{t}\:=\:−\frac{\mathrm{9}}{\mathrm{8}} \\ $$$$\mathrm{3}{t}\:=\:\mathrm{3}{x}\:+\:\mathrm{3}{y}\:+\:\mathrm{3}{z} \\ $$$$\:\:\:\:\:=\:\mathrm{3}{x}\:+\:\mathrm{3}{y}\:+\:{x}^{\mathrm{2}} \:+\:\mathrm{2}{y}^{\mathrm{2}} \\ $$$$\:\:\:\:\:=\:\left({x}\:+\:\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\:\mathrm{2}\left({y}\:+\:\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} \:−\:\frac{\mathrm{27}}{\mathrm{8}} \\ $$$$\mathrm{In}\:\mathrm{order}\:\mathrm{to}\:\mathrm{have}\:\mathrm{only}\:\mathrm{a}\:\mathrm{three}−\mathrm{ordered}−\mathrm{pair}\:\mathrm{solution}, \\ $$$$\mathrm{so}\:\mathrm{must}\:\mathrm{be}\:\mathrm{3}{t}\:=\:−\:\frac{\mathrm{27}}{\mathrm{8}}\:\Leftrightarrow\:{t}\:=\:−\:\frac{\mathrm{9}}{\mathrm{8}} \\ $$$$ \\ $$$$\mathrm{Is}\:\mathrm{there}\:\mathrm{anyone}\:\mathrm{who}\:\mathrm{can}\:\mathrm{explain}\:\mathrm{that}\:\mathrm{explanation}\:\mathrm{above}? \\ $$
Answered by mrW1 last updated on 13/Mar/17
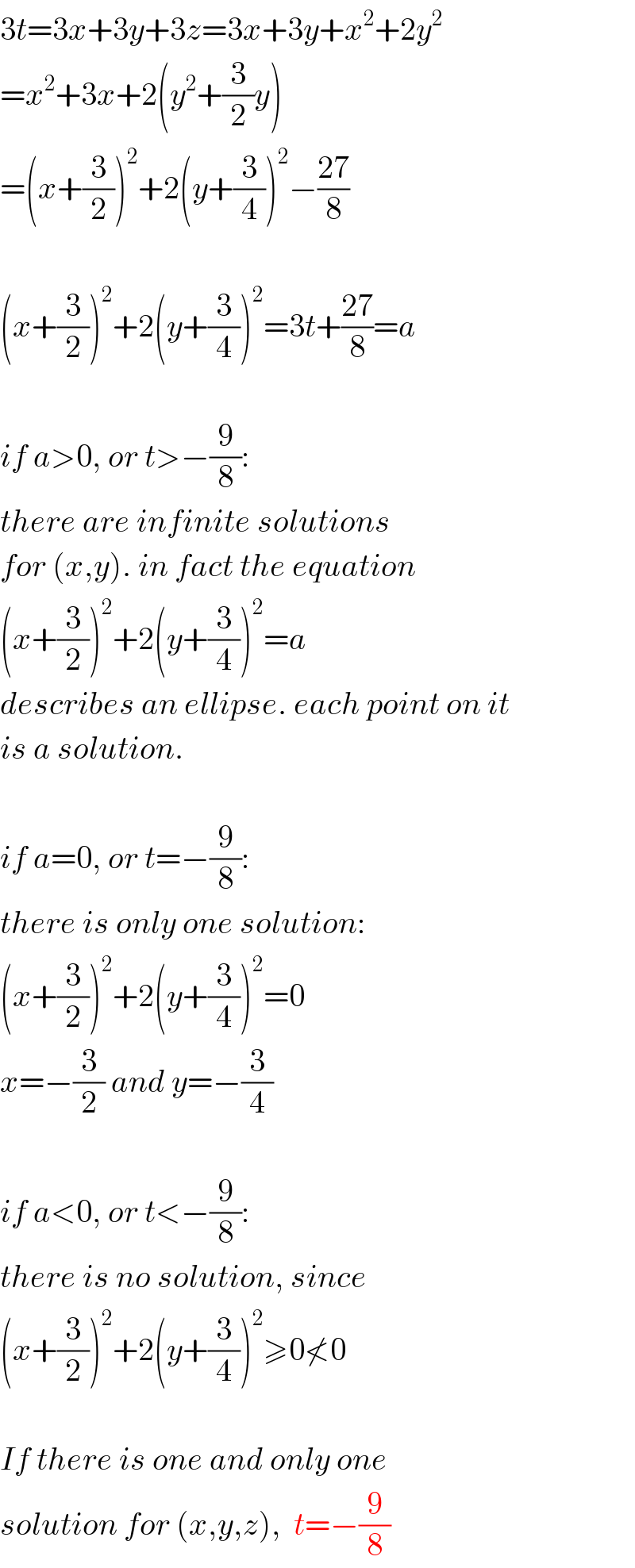
3t=3x+3y+3z=3x+3y+x^2 +2y^2 =x^2 +3x+2(y^2 +(3/2)y) =(x+(3/2))^2 +2(y+(3/4))^2 −((27)/8) (x+(3/2))^2 +2(y+(3/4))^2 =3t+((27)/8)=a if a>0, or t>−(9/8): there are infinite solutions for (x,y). in fact the equation (x+(3/2))^2 +2(y+(3/4))^2 =a describes an ellipse. each point on it is a solution. if a=0, or t=−(9/8): there is only one solution: (x+(3/2))^2 +2(y+(3/4))^2 =0 x=−(3/2) and y=−(3/4) if a<0, or t<−(9/8): there is no solution, since (x+(3/2))^2 +2(y+(3/4))^2 ≥0≮0 If there is one and only one solution for (x,y,z), t=−(9/8)
$$\mathrm{3}{t}=\mathrm{3}{x}+\mathrm{3}{y}+\mathrm{3}{z}=\mathrm{3}{x}+\mathrm{3}{y}+{x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} \\ $$$$={x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{2}\left({y}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{2}}{y}\right) \\ $$$$=\left({x}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{2}\left({y}+\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} −\frac{\mathrm{27}}{\mathrm{8}} \\ $$$$ \\ $$$$\left({x}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{2}\left({y}+\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} =\mathrm{3}{t}+\frac{\mathrm{27}}{\mathrm{8}}={a} \\ $$$$ \\ $$$${if}\:{a}>\mathrm{0},\:{or}\:{t}>−\frac{\mathrm{9}}{\mathrm{8}}: \\ $$$${there}\:{are}\:{infinite}\:{solutions} \\ $$$${for}\:\left({x},{y}\right).\:{in}\:{fact}\:{the}\:{equation} \\ $$$$\left({x}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{2}\left({y}+\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} ={a} \\ $$$${describes}\:{an}\:{ellipse}.\:{each}\:{point}\:{on}\:{it} \\ $$$${is}\:{a}\:{solution}. \\ $$$$ \\ $$$${if}\:{a}=\mathrm{0},\:{or}\:{t}=−\frac{\mathrm{9}}{\mathrm{8}}: \\ $$$${there}\:{is}\:{only}\:{one}\:{solution}: \\ $$$$\left({x}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{2}\left({y}+\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${x}=−\frac{\mathrm{3}}{\mathrm{2}}\:{and}\:{y}=−\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$ \\ $$$${if}\:{a}<\mathrm{0},\:{or}\:{t}<−\frac{\mathrm{9}}{\mathrm{8}}: \\ $$$${there}\:{is}\:{no}\:{solution},\:{since}\: \\ $$$$\left({x}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{2}\left({y}+\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} \geqslant\mathrm{0}\nless\mathrm{0} \\ $$$$ \\ $$$${If}\:{there}\:{is}\:{one}\:{and}\:{only}\:{one} \\ $$$${solution}\:{for}\:\left({x},{y},{z}\right),\:\:{t}=−\frac{\mathrm{9}}{\mathrm{8}} \\ $$
Commented by Joel576 last updated on 13/Mar/17
thank you very much
$${thank}\:{you}\:{very}\:{much} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *