Menu Close

Question-11166

Tinku Tara 0 Comments
Pin




Question Number 11166 by chux last updated on 14/Mar/17
Commented by ridwan balatif last updated on 15/Mar/17
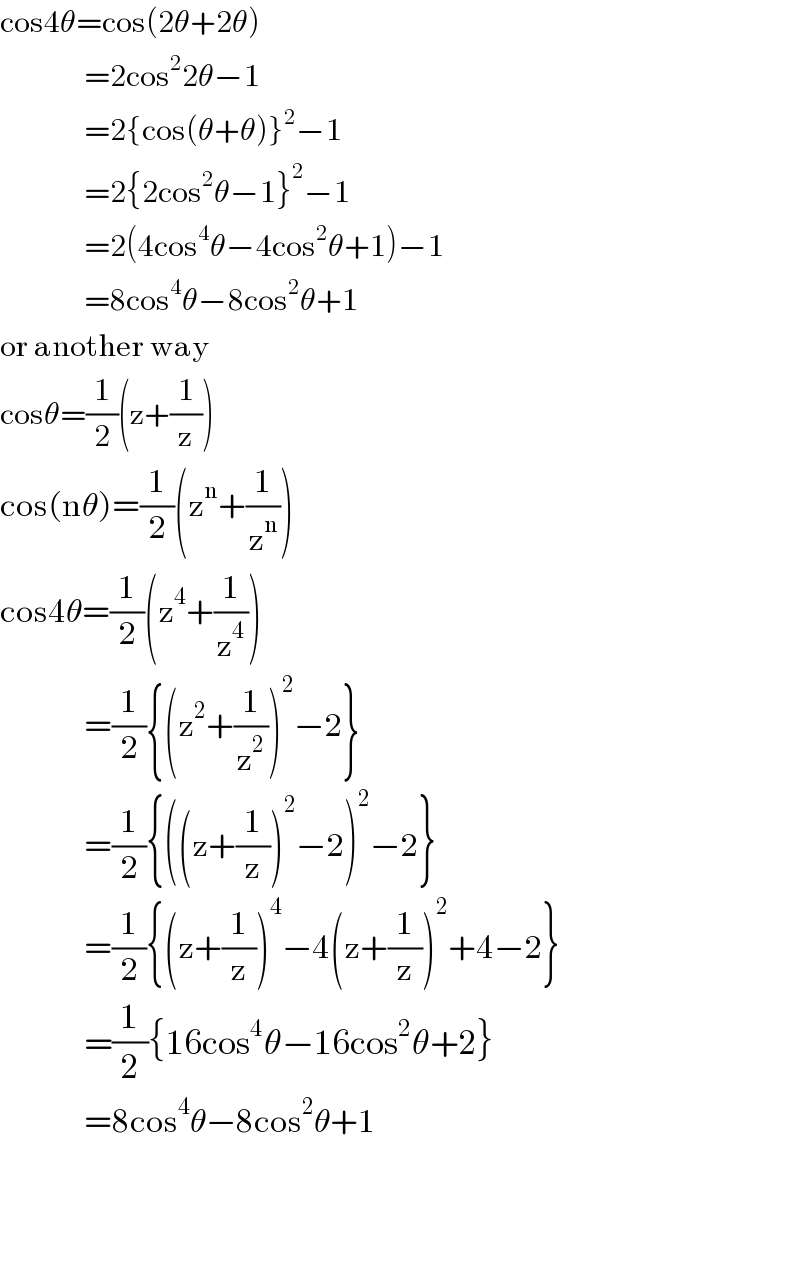
cos4θ=cos(2θ+2θ) =2cos^2 2θ−1 =2{cos(θ+θ)}^2 −1 =2{2cos^2 θ−1}^2 −1 =2(4cos^4 θ−4cos^2 θ+1)−1 =8cos^4 θ−8cos^2 θ+1 or another way cosθ=(1/2)(z+(1/z)) cos(nθ)=(1/2)(z^n +(1/z^n )) cos4θ=(1/2)(z^4 +(1/z^4 )) =(1/2){(z^2 +(1/z^2 ))^2 −2} =(1/2){((z+(1/z))^2 −2)^2 −2} =(1/2){(z+(1/z))^4 −4(z+(1/z))^2 +4−2} =(1/2){16cos^4 θ−16cos^2 θ+2} =8cos^4 θ−8cos^2 θ+1
$$\mathrm{cos4}\theta=\mathrm{cos}\left(\mathrm{2}\theta+\mathrm{2}\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2cos}^{\mathrm{2}} \mathrm{2}\theta−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left\{\mathrm{cos}\left(\theta+\theta\right)\right\}^{\mathrm{2}} −\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left\{\mathrm{2cos}^{\mathrm{2}} \theta−\mathrm{1}\right\}^{\mathrm{2}} −\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left(\mathrm{4cos}^{\mathrm{4}} \theta−\mathrm{4cos}^{\mathrm{2}} \theta+\mathrm{1}\right)−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{8cos}^{\mathrm{4}} \theta−\mathrm{8cos}^{\mathrm{2}} \theta+\mathrm{1} \\ $$$$\mathrm{or}\:\mathrm{another}\:\mathrm{way} \\ $$$$\mathrm{cos}\theta=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{z}+\frac{\mathrm{1}}{\mathrm{z}}\right) \\ $$$$\mathrm{cos}\left(\mathrm{n}\theta\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{z}^{\mathrm{n}} +\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{n}} }\right) \\ $$$$\mathrm{cos4}\theta=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{z}^{\mathrm{4}} +\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{4}} }\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\left(\mathrm{z}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} }\right)^{\mathrm{2}} −\mathrm{2}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\left(\left(\mathrm{z}+\frac{\mathrm{1}}{\mathrm{z}}\right)^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\left(\mathrm{z}+\frac{\mathrm{1}}{\mathrm{z}}\right)^{\mathrm{4}} −\mathrm{4}\left(\mathrm{z}+\frac{\mathrm{1}}{\mathrm{z}}\right)^{\mathrm{2}} +\mathrm{4}−\mathrm{2}\right\}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{16cos}^{\mathrm{4}} \theta−\mathrm{16cos}^{\mathrm{2}} \theta+\mathrm{2}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{8cos}^{\mathrm{4}} \theta−\mathrm{8cos}^{\mathrm{2}} \theta+\mathrm{1} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by ajfour last updated on 15/Mar/17
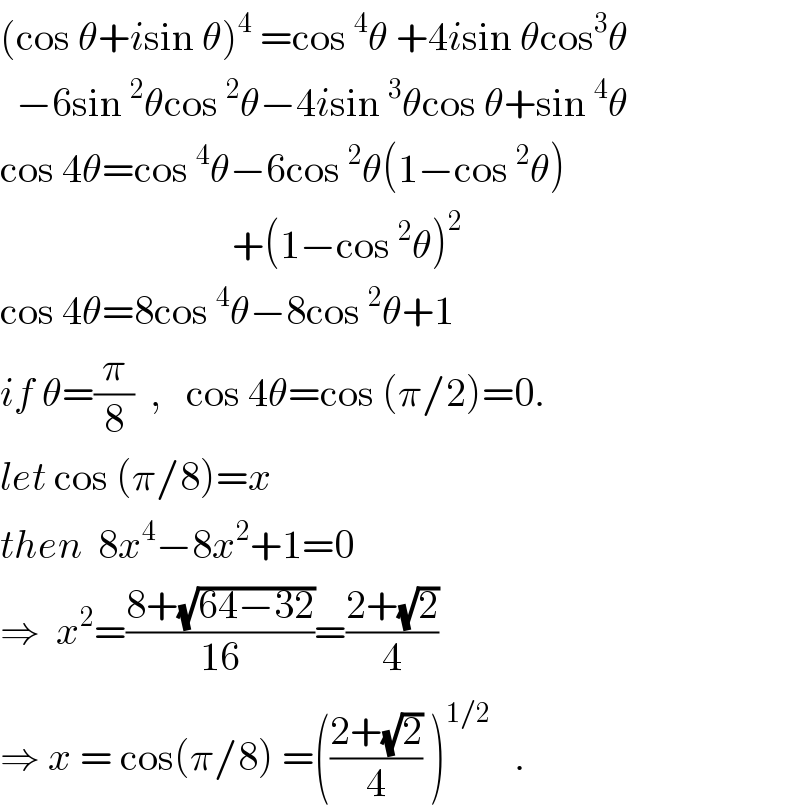
(cos θ+isin θ)^4 =cos^4 θ +4isin θcos^3 θ −6sin^2 θcos^2 θ−4isin^3 θcos θ+sin^4 θ cos 4θ=cos^4 θ−6cos^2 θ(1−cos^2 θ) +(1−cos^2 θ)^2 cos 4θ=8cos^4 θ−8cos^2 θ+1 if θ=(π/8) , cos 4θ=cos (π/2)=0. let cos (π/8)=x then 8x^4 −8x^2 +1=0 ⇒ x^2 =((8+(√(64−32)))/(16))=((2+(√2))/4) ⇒ x = cos(π/8) =(((2+(√2))/4) )^(1/2) .
$$\left(\mathrm{cos}\:\theta+{i}\mathrm{sin}\:\theta\right)^{\mathrm{4}} \:=\mathrm{cos}\:^{\mathrm{4}} \theta\:+\mathrm{4}{i}\mathrm{sin}\:\theta\mathrm{cos}^{\mathrm{3}} \theta \\ $$$$\:\:−\mathrm{6sin}\:^{\mathrm{2}} \theta\mathrm{cos}\:^{\mathrm{2}} \theta−\mathrm{4}{i}\mathrm{sin}\:^{\mathrm{3}} \theta\mathrm{cos}\:\theta+\mathrm{sin}\:^{\mathrm{4}} \theta \\ $$$$\mathrm{cos}\:\mathrm{4}\theta=\mathrm{cos}\:^{\mathrm{4}} \theta−\mathrm{6cos}\:^{\mathrm{2}} \theta\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \theta\right)^{\mathrm{2}} \\ $$$$\mathrm{cos}\:\mathrm{4}\theta=\mathrm{8cos}\:^{\mathrm{4}} \theta−\mathrm{8cos}\:^{\mathrm{2}} \theta+\mathrm{1} \\ $$$${if}\:\theta=\frac{\pi}{\mathrm{8}}\:\:,\:\:\:\mathrm{cos}\:\mathrm{4}\theta=\mathrm{cos}\:\left(\pi/\mathrm{2}\right)=\mathrm{0}. \\ $$$${let}\:\mathrm{cos}\:\left(\pi/\mathrm{8}\right)={x} \\ $$$${then}\:\:\mathrm{8}{x}^{\mathrm{4}} −\mathrm{8}{x}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:{x}^{\mathrm{2}} =\frac{\mathrm{8}+\sqrt{\mathrm{64}−\mathrm{32}}}{\mathrm{16}}=\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$$$\Rightarrow\:{x}\:=\:\mathrm{cos}\left(\pi/\mathrm{8}\right)\:=\left(\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{4}}\:\right)^{\mathrm{1}/\mathrm{2}} \:\:\:. \\ $$
Commented by chux last updated on 15/Mar/17
thanks alot...... it really helps.
$$\mathrm{thanks}\:\mathrm{alot}……\:\mathrm{it}\:\mathrm{really}\:\mathrm{helps}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *