Question Number 11183 by Nayon last updated on 15/Mar/17
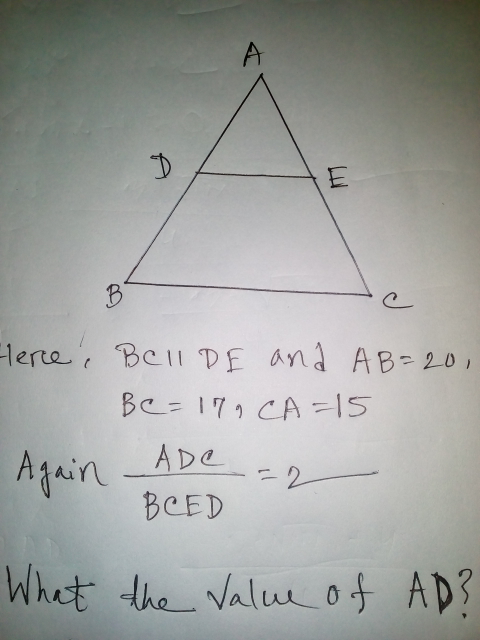
Answered by mrW1 last updated on 16/Mar/17
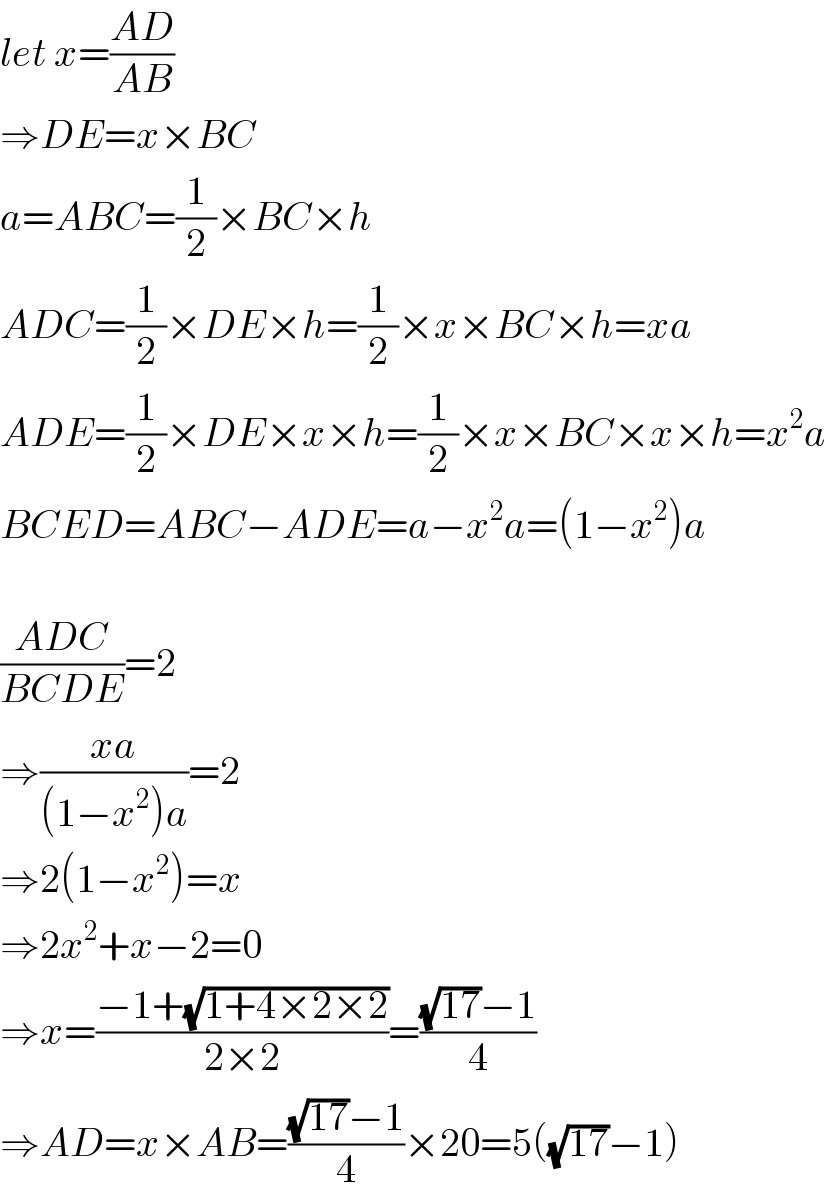
$${let}\:{x}=\frac{{AD}}{{AB}} \\ $$$$\Rightarrow{DE}={x}×{BC} \\ $$$${a}={ABC}=\frac{\mathrm{1}}{\mathrm{2}}×{BC}×{h} \\ $$$${ADC}=\frac{\mathrm{1}}{\mathrm{2}}×{DE}×{h}=\frac{\mathrm{1}}{\mathrm{2}}×{x}×{BC}×{h}={xa} \\ $$$${ADE}=\frac{\mathrm{1}}{\mathrm{2}}×{DE}×{x}×{h}=\frac{\mathrm{1}}{\mathrm{2}}×{x}×{BC}×{x}×{h}={x}^{\mathrm{2}} {a} \\ $$$${BCED}={ABC}−{ADE}={a}−{x}^{\mathrm{2}} {a}=\left(\mathrm{1}−{x}^{\mathrm{2}} \right){a} \\ $$$$ \\ $$$$\frac{{ADC}}{{BCDE}}=\mathrm{2} \\ $$$$\Rightarrow\frac{{xa}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right){a}}=\mathrm{2} \\ $$$$\Rightarrow\mathrm{2}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)={x} \\ $$$$\Rightarrow\mathrm{2}{x}^{\mathrm{2}} +{x}−\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{−\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}×\mathrm{2}×\mathrm{2}}}{\mathrm{2}×\mathrm{2}}=\frac{\sqrt{\mathrm{17}}−\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow{AD}={x}×{AB}=\frac{\sqrt{\mathrm{17}}−\mathrm{1}}{\mathrm{4}}×\mathrm{20}=\mathrm{5}\left(\sqrt{\mathrm{17}}−\mathrm{1}\right) \\ $$
Commented by Nayon last updated on 16/Mar/17

$$\left.\right\} \\ $$
Commented by mrW1 last updated on 16/Mar/17
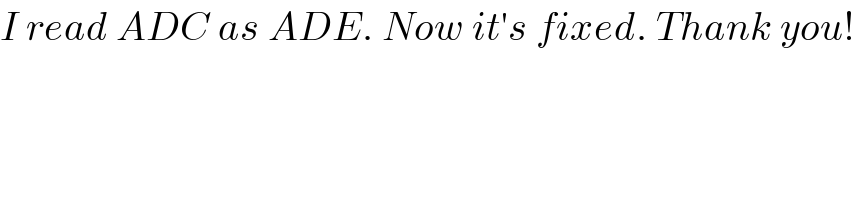
$${I}\:{read}\:{ADC}\:{as}\:{ADE}.\:{Now}\:{it}'{s}\:{fixed}.\:{Thank}\:{you}! \\ $$
Commented by Nayon last updated on 16/Mar/17

$${Thank}\:{you}\:{mr}.{w}\mathrm{1} \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 16/Mar/17

$${hello}\:{mrW}\mathrm{1}.\:{the}\:{answer}\:{of}\:{Q}.{n}:\mathrm{10455} \\ $$$${is}\:{posted}.{please}\:{check}\:{it}\:{and}\:{post}\:{your} \\ $$$${communt}\:{about}\:{it}\:.{thank}\:{you}\:{very}\:{much}. \\ $$
Commented by Nayon last updated on 16/Mar/17
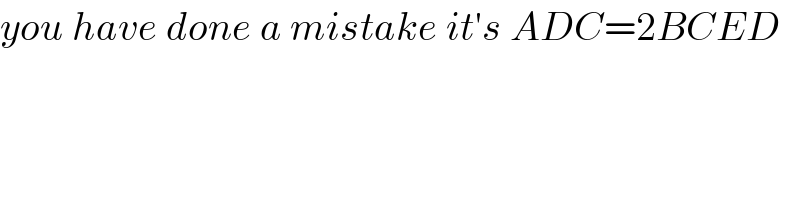
$${you}\:{have}\:{done}\:{a}\:{mistake}\:{it}'{s}\:{ADC}=\mathrm{2}{BCED} \\ $$
