Question Number 11416 by anisa last updated on 25/Mar/17

Answered by Joel576 last updated on 25/Mar/17
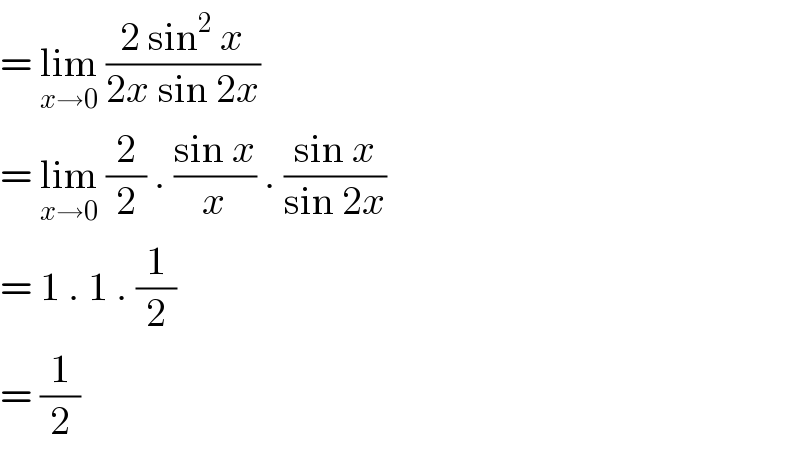
$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:{x}}{\mathrm{2}{x}\:\mathrm{sin}\:\mathrm{2}{x}} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}}{\mathrm{2}}\:.\:\frac{\mathrm{sin}\:{x}}{{x}}\:.\:\frac{\mathrm{sin}\:{x}}{\mathrm{sin}\:\mathrm{2}{x}} \\ $$$$=\:\mathrm{1}\:.\:\mathrm{1}\:.\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
