Menu Close

Question-11536

Tinku Tara 0 Comments
Pin




Question Number 11536 by tawa last updated on 27/Mar/17
Answered by ridwan balatif last updated on 28/Mar/17
Data: m=0.140kg, v_o =25m/s (a) EK=(1/2)mv_o ^2 =(1/2)×0.140×25^2 =43.75J (b)if the ball wanna reach maximum height it′s velocity at maximum height must be zero (v_t =0) v_t ^2 =v_o ^2 −2gh 0^2 =25^2 −2×10×h h =32.5 m (c)v^2 =v_o ^2 −2gh v^2 =25^2 −2×10×30 v=5m/s EK=(1/2)mv^2 =(1/2)×0.14×5^2 =1.75J
$$\mathrm{Data}:\:\mathrm{m}=\mathrm{0}.\mathrm{140kg},\:\:{v}_{\mathrm{o}} =\mathrm{25m}/\mathrm{s} \\ $$$$\left(\mathrm{a}\right)\:\mathrm{EK}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{m}{v}_{\mathrm{o}} ^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{0}.\mathrm{140}×\mathrm{25}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{43}.\mathrm{75J} \\ $$$$\left(\mathrm{b}\right)\mathrm{if}\:\mathrm{the}\:\mathrm{ball}\:\mathrm{wanna}\:\mathrm{reach}\:\mathrm{maximum}\:\mathrm{height}\: \\ $$$$\:\:\:\:\:\:\:\mathrm{it}'\mathrm{s}\:\mathrm{velocity}\:\mathrm{at}\:\mathrm{maximum}\:\mathrm{height}\:\mathrm{must}\:\mathrm{be}\:\mathrm{zero}\:\left({v}_{\mathrm{t}} =\mathrm{0}\right) \\ $$$${v}_{{t}} ^{\mathrm{2}} ={v}_{\mathrm{o}} ^{\mathrm{2}} −\mathrm{2}{gh} \\ $$$$\mathrm{0}^{\mathrm{2}} =\mathrm{25}^{\mathrm{2}} −\mathrm{2}×\mathrm{10}×{h} \\ $$$${h}\:=\mathrm{32}.\mathrm{5}\:{m} \\ $$$$\left(\mathrm{c}\right){v}^{\mathrm{2}} ={v}_{{o}} ^{\mathrm{2}} −\mathrm{2}{g}\mathrm{h} \\ $$$$\:\:\:\:\:\:\:{v}^{\mathrm{2}} =\mathrm{25}^{\mathrm{2}} −\mathrm{2}×\mathrm{10}×\mathrm{30} \\ $$$$\:\:\:\:\:\:\:\:\:{v}=\mathrm{5m}/\mathrm{s} \\ $$$$\mathrm{EK}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{m}{v}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{0}.\mathrm{14}×\mathrm{5}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{1}.\mathrm{75J} \\ $$$$ \\ $$
Commented by tawa last updated on 28/Mar/17
I really appreciate sir. God bless you.
$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
Answered by Nysiroke last updated on 28/Mar/17
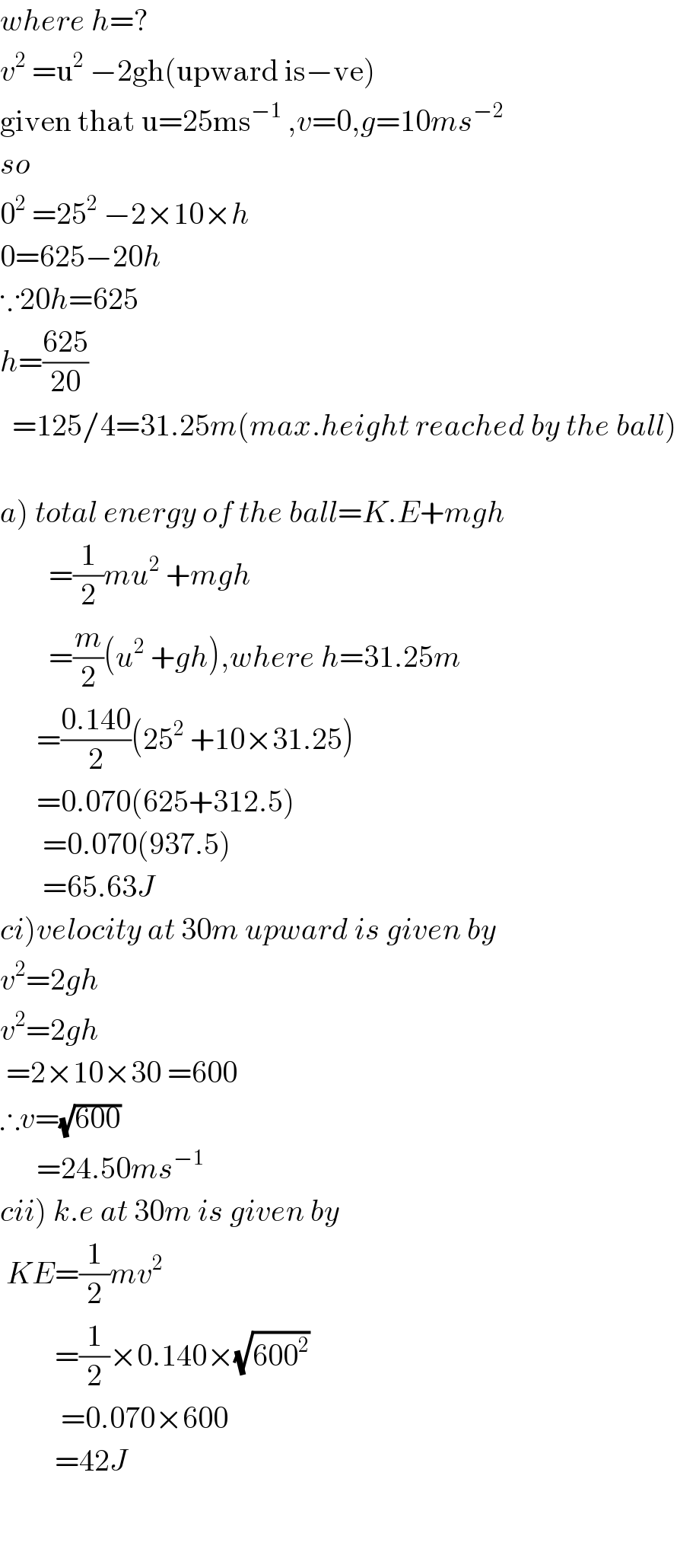
where h=? v^2 =u^2 −2gh(upward is−ve) given that u=25ms^(−1) ,v=0,g=10ms^(−2) so 0^2 =25^2 −2×10×h 0=625−20h ∵20h=625 h=((625)/(20)) =125/4=31.25m(max.height reached by the ball) a) total energy of the ball=K.E+mgh =(1/2)mu^2 +mgh =(m/2)(u^2 +gh),where h=31.25m =((0.140)/2)(25^2 +10×31.25) =0.070(625+312.5) =0.070(937.5) =65.63J ci)velocity at 30m upward is given by v^2 =2gh v^2 =2gh =2×10×30 =600 ∴v=(√(600)) =24.50ms^(−1) cii) k.e at 30m is given by KE=(1/2)mv^2 =(1/2)×0.140×(√(600^2 )) =0.070×600 =42J
$${where}\:{h}=? \\ $$$${v}^{\mathrm{2}} \:=\mathrm{u}^{\mathrm{2}} \:−\mathrm{2gh}\left(\mathrm{upward}\:\mathrm{is}−\mathrm{ve}\right) \\ $$$$\mathrm{given}\:\mathrm{that}\:\mathrm{u}=\mathrm{25ms}^{−\mathrm{1}} \:,{v}=\mathrm{0},{g}=\mathrm{10}{ms}^{−\mathrm{2}} \\ $$$${so} \\ $$$$\mathrm{0}^{\mathrm{2}} \:=\mathrm{25}^{\mathrm{2}} \:−\mathrm{2}×\mathrm{10}×{h} \\ $$$$\mathrm{0}=\mathrm{625}−\mathrm{20}{h} \\ $$$$\because\mathrm{20}{h}=\mathrm{625} \\ $$$${h}=\frac{\mathrm{625}}{\mathrm{20}} \\ $$$$\:\:=\mathrm{125}/\mathrm{4}=\mathrm{31}.\mathrm{25}{m}\left({max}.{height}\:{reached}\:{by}\:{the}\:{ball}\right) \\ $$$$ \\ $$$$\left.{a}\right)\:{total}\:{energy}\:{of}\:{the}\:{ball}={K}.{E}+{mgh} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}{mu}^{\mathrm{2}} \:+{mgh} \\ $$$$\:\:\:\:\:\:\:\:=\frac{{m}}{\mathrm{2}}\left({u}^{\mathrm{2}} \:+{gh}\right),{where}\:{h}=\mathrm{31}.\mathrm{25}{m} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{0}.\mathrm{140}}{\mathrm{2}}\left(\mathrm{25}^{\mathrm{2}} \:+\mathrm{10}×\mathrm{31}.\mathrm{25}\right) \\ $$$$\:\:\:\:\:\:=\mathrm{0}.\mathrm{070}\left(\mathrm{625}+\mathrm{312}.\mathrm{5}\right) \\ $$$$\:\:\:\:\:\:\:=\mathrm{0}.\mathrm{070}\left(\mathrm{937}.\mathrm{5}\right) \\ $$$$\:\:\:\:\:\:\:=\mathrm{65}.\mathrm{63}{J} \\ $$$$\left.{ci}\right){velocity}\:{at}\:\mathrm{30}{m}\:{upward}\:{is}\:{given}\:{by} \\ $$$${v}^{\mathrm{2}} =\mathrm{2}{gh} \\ $$$${v}^{\mathrm{2}} =\mathrm{2}{gh} \\ $$$$\:=\mathrm{2}×\mathrm{10}×\mathrm{30}\:=\mathrm{600} \\ $$$$\therefore{v}=\sqrt{\mathrm{600}} \\ $$$$\:\:\:\:\:\:=\mathrm{24}.\mathrm{50}{ms}^{−\mathrm{1}} \\ $$$$\left.{cii}\right)\:{k}.{e}\:{at}\:\mathrm{30}{m}\:{is}\:{given}\:{by} \\ $$$$\:{KE}=\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{0}.\mathrm{140}×\sqrt{\mathrm{600}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{0}.\mathrm{070}×\mathrm{600} \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{42}{J} \\ $$$$\:\:\:\: \\ $$$$ \\ $$
Commented by tawa last updated on 28/Mar/17
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *