Menu Close

Question-11915

Tinku Tara 0 Comments
Pin




Question Number 11915 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 04/Apr/17
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 04/Apr/17
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 04/Apr/17
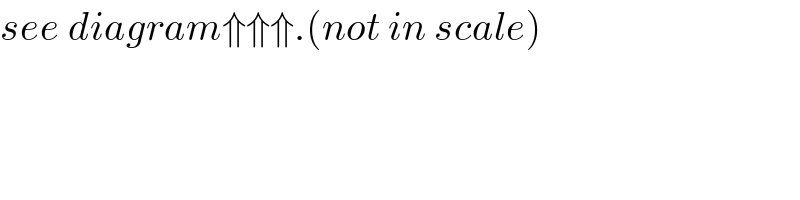
see diagram⇑⇑⇑.(not in scale)
$${see}\:{diagram}\Uparrow\Uparrow\Uparrow.\left({not}\:{in}\:{scale}\right) \\ $$
Answered by mrW1 last updated on 05/Apr/17
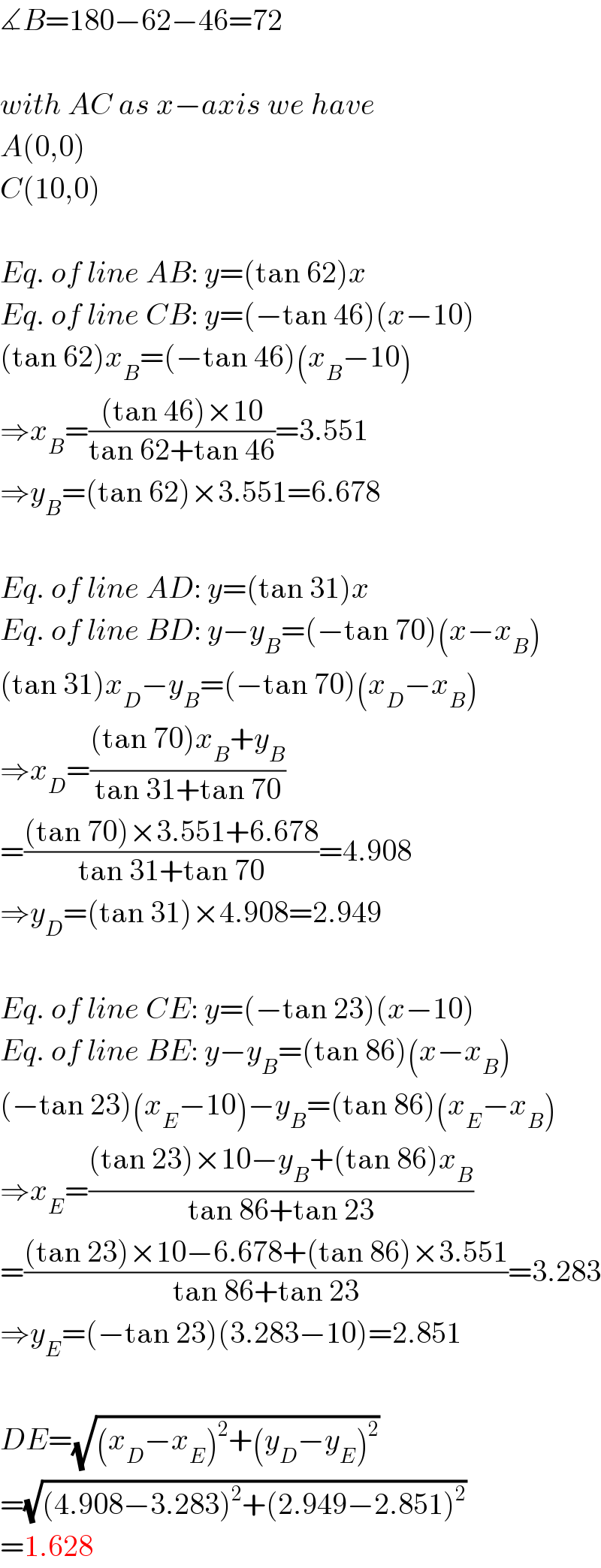
∡B=180−62−46=72 with AC as x−axis we have A(0,0) C(10,0) Eq. of line AB: y=(tan 62)x Eq. of line CB: y=(−tan 46)(x−10) (tan 62)x_B =(−tan 46)(x_B −10) ⇒x_B =(((tan 46)×10)/(tan 62+tan 46))=3.551 ⇒y_B =(tan 62)×3.551=6.678 Eq. of line AD: y=(tan 31)x Eq. of line BD: y−y_B =(−tan 70)(x−x_B ) (tan 31)x_D −y_B =(−tan 70)(x_D −x_B ) ⇒x_D =(((tan 70)x_B +y_B )/(tan 31+tan 70)) =(((tan 70)×3.551+6.678)/(tan 31+tan 70))=4.908 ⇒y_D =(tan 31)×4.908=2.949 Eq. of line CE: y=(−tan 23)(x−10) Eq. of line BE: y−y_B =(tan 86)(x−x_B ) (−tan 23)(x_E −10)−y_B =(tan 86)(x_E −x_B ) ⇒x_E =(((tan 23)×10−y_B +(tan 86)x_B )/(tan 86+tan 23)) =(((tan 23)×10−6.678+(tan 86)×3.551)/(tan 86+tan 23))=3.283 ⇒y_E =(−tan 23)(3.283−10)=2.851 DE=(√((x_D −x_E )^2 +(y_D −y_E )^2 )) =(√((4.908−3.283)^2 +(2.949−2.851)^2 )) =1.628
$$\measuredangle{B}=\mathrm{180}−\mathrm{62}−\mathrm{46}=\mathrm{72} \\ $$$$ \\ $$$${with}\:{AC}\:{as}\:{x}−{axis}\:{we}\:{have} \\ $$$${A}\left(\mathrm{0},\mathrm{0}\right) \\ $$$${C}\left(\mathrm{10},\mathrm{0}\right) \\ $$$$ \\ $$$${Eq}.\:{of}\:{line}\:{AB}:\:{y}=\left(\mathrm{tan}\:\mathrm{62}\right){x} \\ $$$${Eq}.\:{of}\:{line}\:{CB}:\:{y}=\left(−\mathrm{tan}\:\mathrm{46}\right)\left({x}−\mathrm{10}\right) \\ $$$$\left(\mathrm{tan}\:\mathrm{62}\right){x}_{{B}} =\left(−\mathrm{tan}\:\mathrm{46}\right)\left({x}_{{B}} −\mathrm{10}\right) \\ $$$$\Rightarrow{x}_{{B}} =\frac{\left(\mathrm{tan}\:\mathrm{46}\right)×\mathrm{10}}{\mathrm{tan}\:\mathrm{62}+\mathrm{tan}\:\mathrm{46}}=\mathrm{3}.\mathrm{551} \\ $$$$\Rightarrow{y}_{{B}} =\left(\mathrm{tan}\:\mathrm{62}\right)×\mathrm{3}.\mathrm{551}=\mathrm{6}.\mathrm{678} \\ $$$$ \\ $$$${Eq}.\:{of}\:{line}\:{AD}:\:{y}=\left(\mathrm{tan}\:\mathrm{31}\right){x} \\ $$$${Eq}.\:{of}\:{line}\:{BD}:\:{y}−{y}_{{B}} =\left(−\mathrm{tan}\:\mathrm{70}\right)\left({x}−{x}_{{B}} \right) \\ $$$$\left(\mathrm{tan}\:\mathrm{31}\right){x}_{{D}} −{y}_{{B}} =\left(−\mathrm{tan}\:\mathrm{70}\right)\left({x}_{{D}} −{x}_{{B}} \right) \\ $$$$\Rightarrow{x}_{{D}} =\frac{\left(\mathrm{tan}\:\mathrm{70}\right){x}_{{B}} +{y}_{{B}} }{\mathrm{tan}\:\mathrm{31}+\mathrm{tan}\:\mathrm{70}} \\ $$$$=\frac{\left(\mathrm{tan}\:\mathrm{70}\right)×\mathrm{3}.\mathrm{551}+\mathrm{6}.\mathrm{678}}{\mathrm{tan}\:\mathrm{31}+\mathrm{tan}\:\mathrm{70}}=\mathrm{4}.\mathrm{908} \\ $$$$\Rightarrow{y}_{{D}} =\left(\mathrm{tan}\:\mathrm{31}\right)×\mathrm{4}.\mathrm{908}=\mathrm{2}.\mathrm{949} \\ $$$$ \\ $$$${Eq}.\:{of}\:{line}\:{CE}:\:{y}=\left(−\mathrm{tan}\:\mathrm{23}\right)\left({x}−\mathrm{10}\right) \\ $$$${Eq}.\:{of}\:{line}\:{BE}:\:{y}−{y}_{{B}} =\left(\mathrm{tan}\:\mathrm{86}\right)\left({x}−{x}_{{B}} \right) \\ $$$$\left(−\mathrm{tan}\:\mathrm{23}\right)\left({x}_{{E}} −\mathrm{10}\right)−{y}_{{B}} =\left(\mathrm{tan}\:\mathrm{86}\right)\left({x}_{{E}} −{x}_{{B}} \right) \\ $$$$\Rightarrow{x}_{{E}} =\frac{\left(\mathrm{tan}\:\mathrm{23}\right)×\mathrm{10}−{y}_{{B}} +\left(\mathrm{tan}\:\mathrm{86}\right){x}_{{B}} }{\mathrm{tan}\:\mathrm{86}+\mathrm{tan}\:\mathrm{23}} \\ $$$$=\frac{\left(\mathrm{tan}\:\mathrm{23}\right)×\mathrm{10}−\mathrm{6}.\mathrm{678}+\left(\mathrm{tan}\:\mathrm{86}\right)×\mathrm{3}.\mathrm{551}}{\mathrm{tan}\:\mathrm{86}+\mathrm{tan}\:\mathrm{23}}=\mathrm{3}.\mathrm{283} \\ $$$$\Rightarrow{y}_{{E}} =\left(−\mathrm{tan}\:\mathrm{23}\right)\left(\mathrm{3}.\mathrm{283}−\mathrm{10}\right)=\mathrm{2}.\mathrm{851} \\ $$$$ \\ $$$${DE}=\sqrt{\left({x}_{{D}} −{x}_{{E}} \right)^{\mathrm{2}} +\left({y}_{{D}} −{y}_{{E}} \right)^{\mathrm{2}} } \\ $$$$=\sqrt{\left(\mathrm{4}.\mathrm{908}−\mathrm{3}.\mathrm{283}\right)^{\mathrm{2}} +\left(\mathrm{2}.\mathrm{949}−\mathrm{2}.\mathrm{851}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{1}.\mathrm{628} \\ $$
Commented by mrW1 last updated on 05/Apr/17
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 06/Apr/17
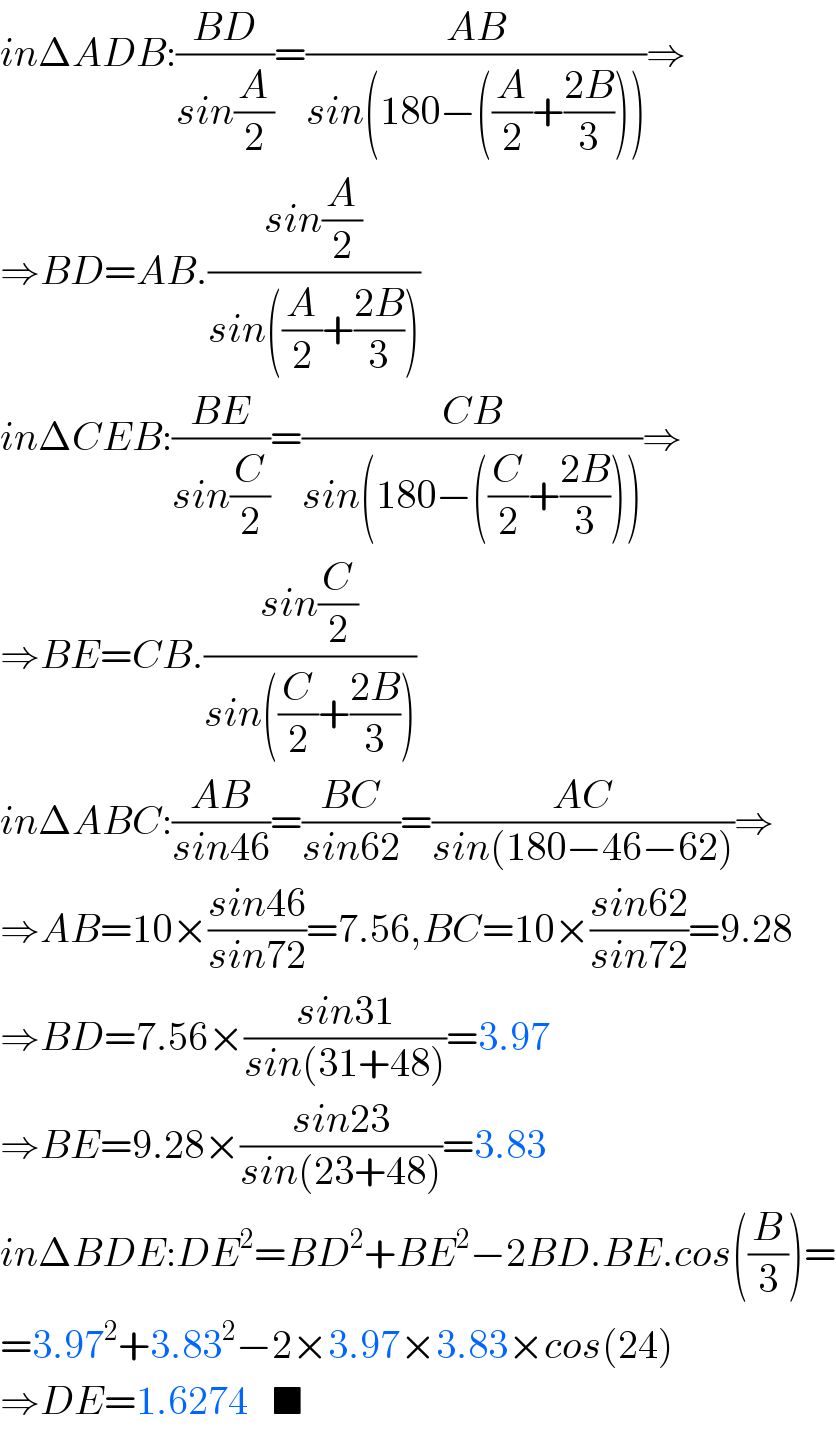
inΔADB:((BD)/(sin(A/2)))=((AB)/(sin(180−((A/2)+((2B)/3)))))⇒ ⇒BD=AB.((sin(A/2))/(sin((A/2)+((2B)/3)))) inΔCEB:((BE)/(sin(C/2)))=((CB)/(sin(180−((C/2)+((2B)/3)))))⇒ ⇒BE=CB.((sin(C/2))/(sin((C/2)+((2B)/3)))) inΔABC:((AB)/(sin46))=((BC)/(sin62))=((AC)/(sin(180−46−62)))⇒ ⇒AB=10×((sin46)/(sin72))=7.56,BC=10×((sin62)/(sin72))=9.28 ⇒BD=7.56×((sin31)/(sin(31+48)))=3.97 ⇒BE=9.28×((sin23)/(sin(23+48)))=3.83 inΔBDE:DE^2 =BD^2 +BE^2 −2BD.BE.cos((B/3))= =3.97^2 +3.83^2 −2×3.97×3.83×cos(24) ⇒DE=1.6274 ■
$${in}\Delta{ADB}:\frac{{BD}}{{sin}\frac{{A}}{\mathrm{2}}}=\frac{{AB}}{{sin}\left(\mathrm{180}−\left(\frac{{A}}{\mathrm{2}}+\frac{\mathrm{2}{B}}{\mathrm{3}}\right)\right)}\Rightarrow \\ $$$$\Rightarrow{BD}={AB}.\frac{{sin}\frac{{A}}{\mathrm{2}}}{{sin}\left(\frac{{A}}{\mathrm{2}}+\frac{\mathrm{2}{B}}{\mathrm{3}}\right)} \\ $$$${in}\Delta{CEB}:\frac{{BE}}{{sin}\frac{{C}}{\mathrm{2}}}=\frac{{CB}}{{sin}\left(\mathrm{180}−\left(\frac{{C}}{\mathrm{2}}+\frac{\mathrm{2}{B}}{\mathrm{3}}\right)\right)}\Rightarrow \\ $$$$\Rightarrow{BE}={CB}.\frac{{sin}\frac{{C}}{\mathrm{2}}}{{sin}\left(\frac{{C}}{\mathrm{2}}+\frac{\mathrm{2}{B}}{\mathrm{3}}\right)} \\ $$$${in}\Delta{ABC}:\frac{{AB}}{{sin}\mathrm{46}}=\frac{{BC}}{{sin}\mathrm{62}}=\frac{{AC}}{{sin}\left(\mathrm{180}−\mathrm{46}−\mathrm{62}\right)}\Rightarrow \\ $$$$\Rightarrow{AB}=\mathrm{10}×\frac{{sin}\mathrm{46}}{{sin}\mathrm{72}}=\mathrm{7}.\mathrm{56},{BC}=\mathrm{10}×\frac{{sin}\mathrm{62}}{{sin}\mathrm{72}}=\mathrm{9}.\mathrm{28} \\ $$$$\Rightarrow{BD}=\mathrm{7}.\mathrm{56}×\frac{{sin}\mathrm{31}}{{sin}\left(\mathrm{31}+\mathrm{48}\right)}=\mathrm{3}.\mathrm{97} \\ $$$$\Rightarrow{BE}=\mathrm{9}.\mathrm{28}×\frac{{sin}\mathrm{23}}{{sin}\left(\mathrm{23}+\mathrm{48}\right)}=\mathrm{3}.\mathrm{83} \\ $$$${in}\Delta{BDE}:{DE}^{\mathrm{2}} ={BD}^{\mathrm{2}} +{BE}^{\mathrm{2}} −\mathrm{2}{BD}.{BE}.{cos}\left(\frac{{B}}{\mathrm{3}}\right)= \\ $$$$=\mathrm{3}.\mathrm{97}^{\mathrm{2}} +\mathrm{3}.\mathrm{83}^{\mathrm{2}} −\mathrm{2}×\mathrm{3}.\mathrm{97}×\mathrm{3}.\mathrm{83}×{cos}\left(\mathrm{24}\right) \\ $$$$\Rightarrow{DE}=\mathrm{1}.\mathrm{6274}\:\:\:\blacksquare \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 07/Apr/17
if any one have another solotion by using geometric or vector methods,please post it here.
$${if}\:{any}\:{one}\:{have}\:{another}\:{solotion}\:{by}\:{using} \\ $$$${geometric}\:{or}\:{vector}\:{methods},{please}\: \\ $$$${post}\:{it}\:{here}. \\ $$
Commented by mrW1 last updated on 05/Apr/17
I used an other way and got a different result, see below.
$${I}\:{used}\:{an}\:{other}\:{way}\:{and}\:{got}\:{a}\:{different} \\ $$$${result},\:{see}\:{below}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 05/Apr/17
thank you very much dear mrW1. you are right.this is my fault.answer is fixed.your method is a bit long. but it is so powerfol and amazing. thanks a lot.
$${thank}\:{you}\:{very}\:{much}\:{dear}\:{mrW}\mathrm{1}. \\ $$$${you}\:{are}\:{right}.{this}\:{is}\:{my}\:{fault}.{answer} \\ $$$${is}\:{fixed}.{your}\:{method}\:{is}\:{a}\:{bit}\:{long}. \\ $$$${but}\:{it}\:{is}\:{so}\:{powerfol}\:{and}\:{amazing}. \\ $$$${thanks}\:{a}\:{lot}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *