Question Number 11998 by ajfour last updated on 09/Apr/17
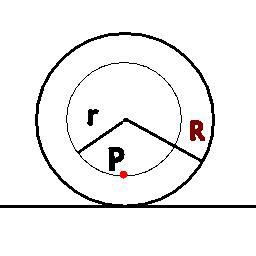
Commented by ajfour last updated on 09/Apr/17

$${What}\:{distance}\:{does}\:{point}\:{P}\: \\ $$$${travel}\:{as}\:{the}\:{centre}\:{moves}\: \\ $$$${forward}\:{by}\:\mathrm{2}\pi{R}\:.\:{The}\:{disc} \\ $$$$\:{rolls}\:{witbout}\:{slipping}\:. \\ $$
Commented by mrW1 last updated on 10/Apr/17
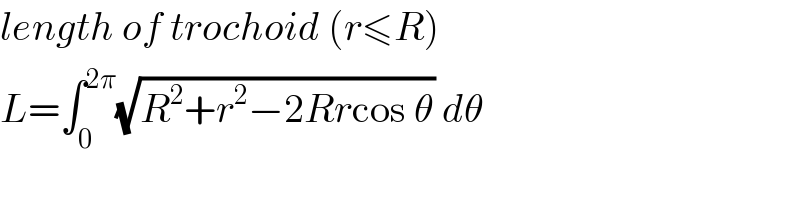
$${length}\:{of}\:{trochoid}\:\left({r}\leqslant{R}\right) \\ $$$${L}=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \sqrt{{R}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{Rr}\mathrm{cos}\:\theta}\:{d}\theta \\ $$
Commented by ajfour last updated on 10/Apr/17

$${thanks},\:{this}\:{is}\:{true}\:{but}\:{couple}\: \\ $$$${of}\:{months}\:{back}\:{you}\:{explained} \\ $$$${solution}\:{to}\:{this}\:{integral}\:{as}\:{well}. \\ $$$${that}\:{dint}\:{seem}\:{to}\:{match}\:{with} \\ $$$${the}\:{case}\:{r}={R}\:{even};\:{for}\:{which} \\ $$$${the}\:{answer}\:{is}\:{L}=\mathrm{8}{R}\:.{Kindly} \\ $$$${solve}\:{this}\:{integral}\:{too}.. \\ $$
Commented by mrW1 last updated on 10/Apr/17

$${For}\:{r}\neq{R}\:{the}\:{integral}\:{is}\:{not}\:{easy}.\: \\ $$$${In}\:{Wolfram}\:{you}\:{can}\:{read}\:{more}\:{details}. \\ $$
