Question Number 12019 by Nayon last updated on 09/Apr/17

Answered by ajfour last updated on 10/Apr/17
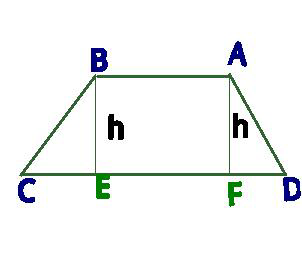
Commented by ajfour last updated on 10/Apr/17
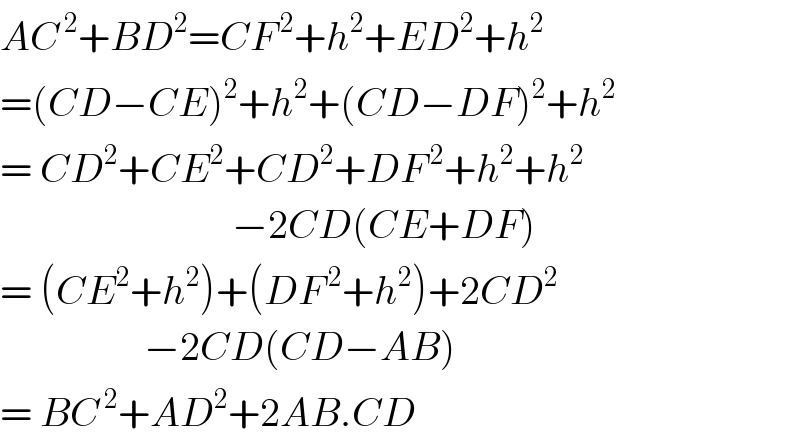
$${AC}^{\:\mathrm{2}} +{BD}^{\mathrm{2}} ={CF}^{\:\mathrm{2}} +{h}^{\mathrm{2}} +{ED}^{\mathrm{2}} +{h}^{\mathrm{2}} \\ $$$$=\left({CD}−{CE}\right)^{\mathrm{2}} +{h}^{\mathrm{2}} +\left({CD}−{DF}\right)^{\mathrm{2}} +{h}^{\mathrm{2}} \\ $$$$=\:{CD}^{\mathrm{2}} +{CE}^{\mathrm{2}} +{CD}^{\mathrm{2}} +{DF}^{\:\mathrm{2}} +{h}^{\mathrm{2}} +{h}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{2}{CD}\left({CE}+{DF}\right) \\ $$$$=\:\left({CE}^{\mathrm{2}} +{h}^{\mathrm{2}} \right)+\left({DF}^{\:\mathrm{2}} +{h}^{\mathrm{2}} \right)+\mathrm{2}{CD}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{2}{CD}\left({CD}−{AB}\right) \\ $$$$=\:{BC}^{\:\mathrm{2}} +{AD}^{\mathrm{2}} +\mathrm{2}{AB}.{CD} \\ $$
