Menu Close

Question-12085

Tinku Tara 0 Comments
Pin




Question Number 12085 by chux last updated on 12/Apr/17
Answered by ajfour last updated on 12/Apr/17
let 6°=θ sin 24°=2sin 12°cos 12° let sin 12°=x and cos 12°=y sin (3θ+2θ)= y sin 18°+x cos 18° ⇒ xcos 18°+ysin 18° =sin 5θ=(1/2) cos (3θ+2θ)=y cos 18°−xsin 18° ⇒ ycos 18°−xsin 18° =cos 5θ=((√3)/2) solve simultaneously for x and y. sin 24°=2xy
$${let}\:\mathrm{6}°=\theta \\ $$$$\mathrm{sin}\:\mathrm{24}°=\mathrm{2sin}\:\mathrm{12}°\mathrm{cos}\:\mathrm{12}° \\ $$$${let}\:\mathrm{sin}\:\mathrm{12}°={x}\:\:{and}\:\:\mathrm{cos}\:\mathrm{12}°={y} \\ $$$$\mathrm{sin}\:\left(\mathrm{3}\theta+\mathrm{2}\theta\right)=\:{y}\:\mathrm{sin}\:\mathrm{18}°+{x}\:\mathrm{cos}\:\mathrm{18}° \\ $$$$\Rightarrow\:{x}\mathrm{cos}\:\mathrm{18}°+{y}\mathrm{sin}\:\mathrm{18}°\:=\mathrm{sin}\:\mathrm{5}\theta=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{cos}\:\left(\mathrm{3}\theta+\mathrm{2}\theta\right)={y}\:\mathrm{cos}\:\mathrm{18}°−{x}\mathrm{sin}\:\mathrm{18}° \\ $$$$\Rightarrow\:{y}\mathrm{cos}\:\mathrm{18}°−{x}\mathrm{sin}\:\mathrm{18}°\:=\mathrm{cos}\:\mathrm{5}\theta=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${solve}\:{simultaneously}\:{for}\:{x}\:{and}\:{y}. \\ $$$$\mathrm{sin}\:\mathrm{24}°=\mathrm{2}{xy} \\ $$
Answered by Joel576 last updated on 16/Apr/17
Let θ = 18 sin 36 = cos 54 sin 2θ = cos 3θ 2 . sin θ. cos θ = 4cos^3 θ − 3cos θ 2sin θ = 4cos^2 θ − 3 2sin θ = 4 − 4sin^2 θ − 3 4sin^2 θ + 2sin θ − 1 = 0 Let sin θ = x 4x^2 + 2x − 1 = 0 x = ((−1 ± (√5))/4) Because θ = 18, so sin 18 = x = (((√5) − 1)/4) cos 18 = (√(1 − sin^2 18)) = (√(1 − ((((√5) − 1)/4))^2 )) = (√(((16)/(16)) − ((5 − 2(√5) + 1)/(16)))) = (√((10 + 2(√5))/(16))) cos 18 = ((√(10 + 2(√5)))/4) cos 48 = cos (30 + 18) = (cos 30 . cos 18) − (sin 30 . sin 18) = (((√3)/2) . ((√(10 + 2(√5)))/4)) − ((1/2) . (((√5) − 1)/4)) = ((√(30 + 6(√5)))/8) − (((√5) − 1)/8) cos 48 = (((√(30 + 6(√5))) − (√5) + 1)/8) Let α = 24 sin α = (√((1 − cos 2α)/2)) = (√((1 − cos 48)/2)) = (√(((8/8) − (((√(30 + 6(√5))) − (√5) + 1)/8))/2)) = (√(((((7 − (√(30 + 6(√5))) + (√5))/8)))/2)) = (√((7 − (√(30 + 6(√5))) + (√5))/(16))) sin 24 = (1/4)((√(7 − (√(30 + 6(√5))) + (√5))))
$$\mathrm{Let}\:\theta\:=\:\mathrm{18} \\ $$$$\mathrm{sin}\:\mathrm{36}\:=\:\mathrm{cos}\:\mathrm{54} \\ $$$$\mathrm{sin}\:\mathrm{2}\theta\:=\:\mathrm{cos}\:\mathrm{3}\theta \\ $$$$\mathrm{2}\:.\:\mathrm{sin}\:\theta.\:\mathrm{cos}\:\theta\:=\:\mathrm{4cos}^{\mathrm{3}} \:\theta\:−\:\mathrm{3cos}\:\theta \\ $$$$\mathrm{2sin}\:\theta\:=\:\mathrm{4cos}^{\mathrm{2}} \:\theta\:−\:\mathrm{3} \\ $$$$\mathrm{2sin}\:\theta\:=\:\mathrm{4}\:−\:\mathrm{4sin}^{\mathrm{2}} \:\theta\:−\:\mathrm{3} \\ $$$$\mathrm{4sin}^{\mathrm{2}} \:\theta\:+\:\mathrm{2sin}\:\theta\:−\:\mathrm{1}\:=\:\mathrm{0} \\ $$$$ \\ $$$$\mathrm{Let}\:\mathrm{sin}\:\theta\:=\:{x} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} \:+\:\mathrm{2}{x}\:−\:\mathrm{1}\:=\:\mathrm{0} \\ $$$${x}\:=\:\frac{−\mathrm{1}\:\pm\:\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\mathrm{Because}\:\theta\:=\:\mathrm{18},\:\mathrm{so}\:\mathrm{sin}\:\mathrm{18}\:=\:{x}\:=\:\frac{\sqrt{\mathrm{5}}\:−\:\mathrm{1}}{\mathrm{4}}\: \\ $$$$\mathrm{cos}\:\mathrm{18}\:=\:\sqrt{\mathrm{1}\:−\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{18}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\sqrt{\mathrm{1}\:−\:\left(\frac{\sqrt{\mathrm{5}}\:−\:\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} }\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\sqrt{\frac{\mathrm{16}}{\mathrm{16}}\:−\:\frac{\mathrm{5}\:−\:\mathrm{2}\sqrt{\mathrm{5}}\:+\:\mathrm{1}}{\mathrm{16}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\sqrt{\frac{\mathrm{10}\:+\:\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{16}}} \\ $$$$\mathrm{cos}\:\mathrm{18}\:=\:\frac{\sqrt{\mathrm{10}\:+\:\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}} \\ $$$$\mathrm{cos}\:\mathrm{48}\:=\:\mathrm{cos}\:\left(\mathrm{30}\:+\:\mathrm{18}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\left(\mathrm{cos}\:\mathrm{30}\:.\:\mathrm{cos}\:\mathrm{18}\right)\:−\:\left(\mathrm{sin}\:\mathrm{30}\:.\:\mathrm{sin}\:\mathrm{18}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:.\:\frac{\sqrt{\mathrm{10}\:+\:\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}}\right)\:−\:\left(\frac{\mathrm{1}}{\mathrm{2}}\:.\:\frac{\sqrt{\mathrm{5}}\:−\:\mathrm{1}}{\mathrm{4}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\sqrt{\mathrm{30}\:+\:\mathrm{6}\sqrt{\mathrm{5}}}}{\mathrm{8}}\:−\:\frac{\sqrt{\mathrm{5}}\:−\:\mathrm{1}}{\mathrm{8}} \\ $$$$\mathrm{cos}\:\mathrm{48}\:=\:\frac{\sqrt{\mathrm{30}\:+\:\mathrm{6}\sqrt{\mathrm{5}}}\:−\:\sqrt{\mathrm{5}}\:+\:\mathrm{1}}{\mathrm{8}} \\ $$$$\mathrm{Let}\:\alpha\:=\:\mathrm{24} \\ $$$$\mathrm{sin}\:\alpha\:=\:\sqrt{\frac{\mathrm{1}\:−\:\mathrm{cos}\:\mathrm{2}\alpha}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\sqrt{\frac{\mathrm{1}\:−\:\mathrm{cos}\:\mathrm{48}}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\sqrt{\frac{\frac{\mathrm{8}}{\mathrm{8}}\:−\:\frac{\sqrt{\mathrm{30}\:+\:\mathrm{6}\sqrt{\mathrm{5}}}\:−\:\sqrt{\mathrm{5}}\:+\:\mathrm{1}}{\mathrm{8}}}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\sqrt{\frac{\left(\frac{\mathrm{7}\:−\:\sqrt{\mathrm{30}\:+\:\mathrm{6}\sqrt{\mathrm{5}}}\:+\:\sqrt{\mathrm{5}}}{\mathrm{8}}\right)}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\sqrt{\frac{\mathrm{7}\:−\:\sqrt{\mathrm{30}\:+\:\mathrm{6}\sqrt{\mathrm{5}}}\:+\:\sqrt{\mathrm{5}}}{\mathrm{16}}} \\ $$$$\mathrm{sin}\:\mathrm{24}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\left(\sqrt{\mathrm{7}\:−\:\sqrt{\mathrm{30}\:+\:\mathrm{6}\sqrt{\mathrm{5}}}\:+\:\sqrt{\mathrm{5}}}\right) \\ $$
Commented by mrW1 last updated on 13/Apr/17
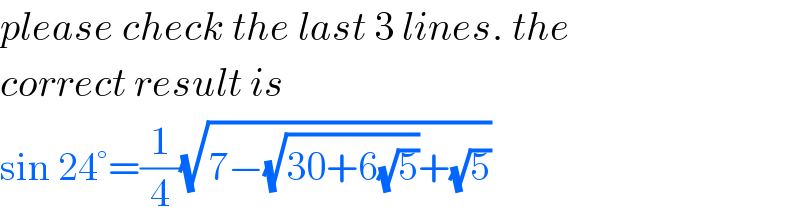
please check the last 3 lines. the correct result is sin 24°=(1/4)(√(7−(√(30+6(√5)))+(√5)))
$${please}\:{check}\:{the}\:{last}\:\mathrm{3}\:{lines}.\:{the} \\ $$$${correct}\:{result}\:{is} \\ $$$$\mathrm{sin}\:\mathrm{24}°=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\mathrm{7}−\sqrt{\mathrm{30}+\mathrm{6}\sqrt{\mathrm{5}}}+\sqrt{\mathrm{5}}} \\ $$
Commented by Joel576 last updated on 16/Apr/17
thank you for correcting my answer. I have fixed that
$${thank}\:{you}\:{for}\:{correcting}\:{my}\:{answer}. \\ $$$${I}\:{have}\:{fixed}\:{that} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *