Question Number 12127 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 13/Apr/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 14/Apr/17
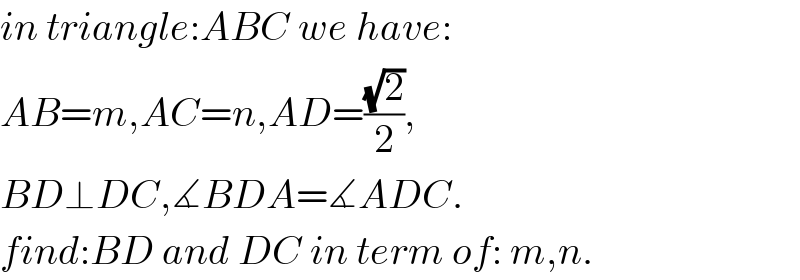
$${in}\:{triangle}:{ABC}\:{we}\:{have}: \\ $$$${AB}={m},{AC}={n},{AD}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}, \\ $$$${BD}\bot{DC},\measuredangle{BDA}=\measuredangle{ADC}. \\ $$$${find}:{BD}\:{and}\:{DC}\:{in}\:{term}\:{of}:\:{m},{n}. \\ $$
Answered by mrW1 last updated on 14/Apr/17
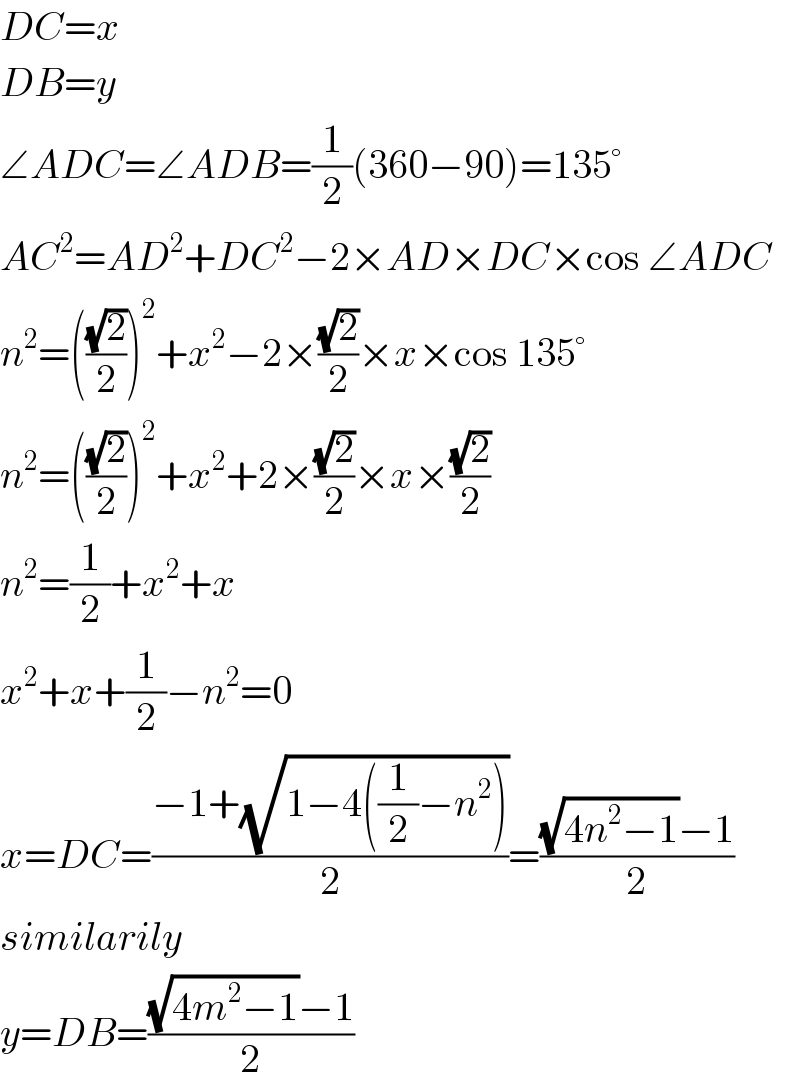
$${DC}={x} \\ $$$${DB}={y} \\ $$$$\angle{ADC}=\angle{ADB}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{360}−\mathrm{90}\right)=\mathrm{135}° \\ $$$${AC}^{\mathrm{2}} ={AD}^{\mathrm{2}} +{DC}^{\mathrm{2}} −\mathrm{2}×{AD}×{DC}×\mathrm{cos}\:\angle{ADC} \\ $$$${n}^{\mathrm{2}} =\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{2}×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}×{x}×\mathrm{cos}\:\mathrm{135}° \\ $$$${n}^{\mathrm{2}} =\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} +\mathrm{2}×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}×{x}×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$${n}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}+{x}^{\mathrm{2}} +{x} \\ $$$${x}^{\mathrm{2}} +{x}+\frac{\mathrm{1}}{\mathrm{2}}−{n}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}={DC}=\frac{−\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{4}\left(\frac{\mathrm{1}}{\mathrm{2}}−{n}^{\mathrm{2}} \right)}}{\mathrm{2}}=\frac{\sqrt{\mathrm{4}{n}^{\mathrm{2}} −\mathrm{1}}−\mathrm{1}}{\mathrm{2}} \\ $$$${similarily} \\ $$$${y}={DB}=\frac{\sqrt{\mathrm{4}{m}^{\mathrm{2}} −\mathrm{1}}−\mathrm{1}}{\mathrm{2}} \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 14/Apr/17

$${thank}\:{you}\:{very}\:{much},\:{dear}\:{mrW}\mathrm{1}. \\ $$
