Question Number 12292 by sin (x) last updated on 18/Apr/17

Answered by mrW1 last updated on 18/Apr/17
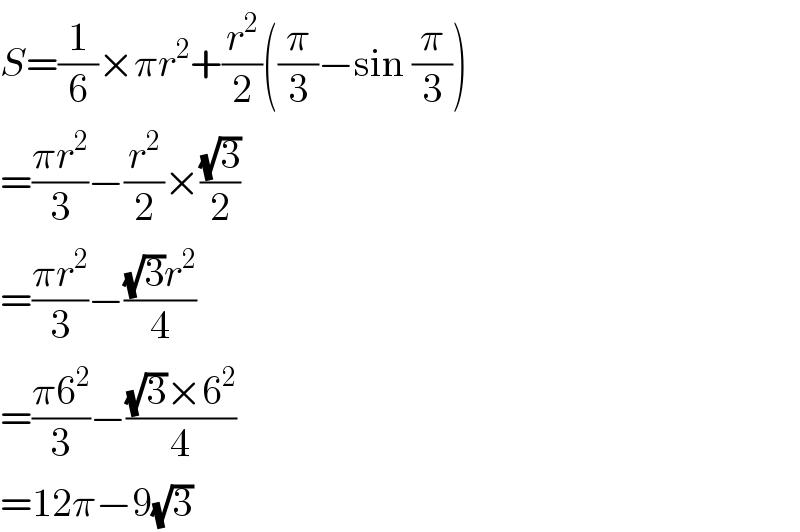
$${S}=\frac{\mathrm{1}}{\mathrm{6}}×\pi{r}^{\mathrm{2}} +\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\pi}{\mathrm{3}}−\mathrm{sin}\:\frac{\pi}{\mathrm{3}}\right) \\ $$$$=\frac{\pi{r}^{\mathrm{2}} }{\mathrm{3}}−\frac{{r}^{\mathrm{2}} }{\mathrm{2}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$=\frac{\pi{r}^{\mathrm{2}} }{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}{r}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$=\frac{\pi\mathrm{6}^{\mathrm{2}} }{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}×\mathrm{6}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$=\mathrm{12}\pi−\mathrm{9}\sqrt{\mathrm{3}} \\ $$
Answered by ajfour last updated on 18/Apr/17

$$=\:\mathrm{2}\left(\frac{\pi{r}^{\mathrm{2}} }{\mathrm{6}}\right)−\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}{r}^{\mathrm{2}} \\ $$$$=\:\mathrm{12}\pi−\mathrm{9}\sqrt{\mathrm{3}}\:. \\ $$
Commented by ajfour last updated on 18/Apr/17

$${sector}\:{area}\:{ABD}\:{witb}\:{centre}\:{A} \\ $$$$\:+{sector}\:{area}\:{BDA}\:{with}\:{centre}\:{B}\: \\ $$$$−\:{area}\:{of}\:\bigtriangleup{ABD}\:. \\ $$
