Question Number 12329 by tawa last updated on 19/Apr/17
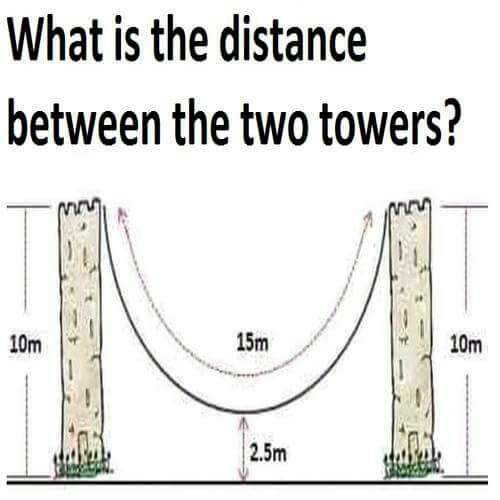
Commented by mrW1 last updated on 19/Apr/17

$${if}\:{the}\:{rope}\:{is}\:{only}\:\mathrm{15}{m}\:{long},\:{the} \\ $$$${distance}\:{between}\:{the}\:{towers}\:{must} \\ $$$${be}\:{zero}! \\ $$
Commented by zainal tanjung last updated on 08/May/20

$$\mathrm{Berapakah}\:\mathrm{jarak}\:\mathrm{kedua}\:\mathrm{tower}\:? \\ $$
Answered by mrW1 last updated on 23/Apr/17
![Solution by assuming the rope curve as catenary. Let′s say the rope length is 25m. Catenary equations with (0,0) at the lowest point of rope: y=a×[cosh ((x/a))−1] s=a×sinh ((x/a)) at x=b: y=a×[cosh ((b/a))−1]=10−2.5=7.5 ⇒cosh ((b/a))=1+((7.5)/a) s=a×sinh ((b/a))=((25)/2)=12.5 ⇒sinh ((b/a))=((12.5)/a) ⇒cosh ((b/a))=1+((7.5)/(12.5))×((12.5)/a)=1+0.6×sinh ((b/a)) ⇒(b/a)≈1.386 ⇒a=((12.5)/(sinh 1.386))=6.669 b=1.386×6.669=9.243 Distance of towers =2×b=18.49 m](https://www.tinkutara.com/question/Q12335.png)
$$\boldsymbol{{Solution}}\:\boldsymbol{{by}}\:\boldsymbol{{assuming}}\:\boldsymbol{{the}}\:\boldsymbol{{rope}}\:\boldsymbol{{curve}} \\ $$$$\boldsymbol{{as}}\:\boldsymbol{{catenary}}. \\ $$$$ \\ $$$${Let}'{s}\:{say}\:{the}\:{rope}\:{length}\:{is}\:\mathrm{25}{m}. \\ $$$$ \\ $$$${Catenary}\:{equations}\:{with}\:\left(\mathrm{0},\mathrm{0}\right)\:{at}\:{the} \\ $$$${lowest}\:{point}\:{of}\:{rope}: \\ $$$${y}={a}×\left[\mathrm{cosh}\:\left(\frac{{x}}{{a}}\right)−\mathrm{1}\right] \\ $$$${s}={a}×\mathrm{sinh}\:\left(\frac{{x}}{{a}}\right) \\ $$$$ \\ $$$${at}\:{x}={b}: \\ $$$${y}={a}×\left[\mathrm{cosh}\:\left(\frac{{b}}{{a}}\right)−\mathrm{1}\right]=\mathrm{10}−\mathrm{2}.\mathrm{5}=\mathrm{7}.\mathrm{5} \\ $$$$\Rightarrow\mathrm{cosh}\:\left(\frac{{b}}{{a}}\right)=\mathrm{1}+\frac{\mathrm{7}.\mathrm{5}}{{a}} \\ $$$${s}={a}×\mathrm{sinh}\:\left(\frac{{b}}{{a}}\right)=\frac{\mathrm{25}}{\mathrm{2}}=\mathrm{12}.\mathrm{5} \\ $$$$\Rightarrow\mathrm{sinh}\:\left(\frac{{b}}{{a}}\right)=\frac{\mathrm{12}.\mathrm{5}}{{a}} \\ $$$$ \\ $$$$\Rightarrow\mathrm{cosh}\:\left(\frac{{b}}{{a}}\right)=\mathrm{1}+\frac{\mathrm{7}.\mathrm{5}}{\mathrm{12}.\mathrm{5}}×\frac{\mathrm{12}.\mathrm{5}}{{a}}=\mathrm{1}+\mathrm{0}.\mathrm{6}×\mathrm{sinh}\:\left(\frac{{b}}{{a}}\right) \\ $$$$\Rightarrow\frac{{b}}{{a}}\approx\mathrm{1}.\mathrm{386} \\ $$$$ \\ $$$$\Rightarrow{a}=\frac{\mathrm{12}.\mathrm{5}}{\mathrm{sinh}\:\mathrm{1}.\mathrm{386}}=\mathrm{6}.\mathrm{669} \\ $$$$ \\ $$$${b}=\mathrm{1}.\mathrm{386}×\mathrm{6}.\mathrm{669}=\mathrm{9}.\mathrm{243} \\ $$$$ \\ $$$${Distance}\:{of}\:{towers}\:=\mathrm{2}×{b}=\mathrm{18}.\mathrm{49}\:{m} \\ $$
Commented by tawa last updated on 19/Apr/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by mrW1 last updated on 22/Apr/17
![Solution by assuming the rope curve as parabola. Length of rope L=25m. Distance between towers l=2b Equation of parabola with (0,0) at the lowest point of rope: y=h((x/b))^2 where h=7.5 m (dy/dx)=((2h)/b^2 )x L=2∫_0 ^b (√(1+((dy/dx))^2 )) dx =2∫_0 ^b (√(1+(((2h)/b^2 )x)^2 )) dx let t=((2hx)/b^2 ) dt=((2h)/b^2 )dx L=2×(b^2 /(2h))∫_0 ^((2h)/b) (√(1+t^2 )) dt =(b^2 /h)∫_0 ^((2h)/b) (√(1+t^2 )) dt=(b^2 /(2h))[t(√(1+t^2 ))+ln (t+(√(1+t^2 )))]_0 ^((2h)/b) =(b^2 /(2h)){(((2h)/b))(√(1+(((2h)/b))^2 ))+ln [(((2h)/b))+(√(1+(((2h)/b))^2 ))]} =((2h)/((((2h)/b))^2 )){(((2h)/b))(√(1+(((2h)/b))^2 ))+ln [(((2h)/b))+(√(1+(((2h)/b))^2 ))]} let α=((2h)/b) L=((2h)/α^2 )[α(√(1+α^2 ))+ln (α+(√(1+α^2 )))] since h=7.5 and L=25 ((15)/α^2 )[α(√(1+α^2 ))+ln (α+(√(1+α^2 )))]=25 α(√(1+α^2 ))+ln (α+(√(1+α^2 )))−((25)/(15))α^2 =0 ⇒α≈1.6 ⇒Distance l=2b=((4h)/α)=((4×7.5)/(1.6))=18.75 m](https://www.tinkutara.com/question/Q12428.png)
$$\boldsymbol{{Solution}}\:\boldsymbol{{by}}\:\boldsymbol{{assuming}}\:\boldsymbol{{the}}\:\boldsymbol{{rope}}\:\boldsymbol{{curve}} \\ $$$$\boldsymbol{{as}}\:\boldsymbol{{parabola}}. \\ $$$$ \\ $$$${Length}\:{of}\:{rope}\:{L}=\mathrm{25}{m}. \\ $$$${Distance}\:{between}\:{towers}\:{l}=\mathrm{2}{b} \\ $$$$ \\ $$$${Equation}\:{of}\:{parabola}\:{with}\:\left(\mathrm{0},\mathrm{0}\right)\:{at} \\ $$$${the}\:{lowest}\:{point}\:{of}\:{rope}: \\ $$$${y}={h}\left(\frac{{x}}{{b}}\right)^{\mathrm{2}} \:{where}\:{h}=\mathrm{7}.\mathrm{5}\:{m} \\ $$$$ \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{2}{h}}{{b}^{\mathrm{2}} }{x} \\ $$$${L}=\mathrm{2}\int_{\mathrm{0}} ^{{b}} \sqrt{\mathrm{1}+\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} }\:{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{{b}} \sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{h}}{{b}^{\mathrm{2}} }{x}\right)^{\mathrm{2}} }\:{dx} \\ $$$${let}\:{t}=\frac{\mathrm{2}{hx}}{{b}^{\mathrm{2}} } \\ $$$${dt}=\frac{\mathrm{2}{h}}{{b}^{\mathrm{2}} }{dx} \\ $$$${L}=\mathrm{2}×\frac{{b}^{\mathrm{2}} }{\mathrm{2}{h}}\int_{\mathrm{0}} ^{\frac{\mathrm{2}{h}}{{b}}} \sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt} \\ $$$$=\frac{{b}^{\mathrm{2}} }{{h}}\int_{\mathrm{0}} ^{\frac{\mathrm{2}{h}}{{b}}} \sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt}=\frac{{b}^{\mathrm{2}} }{\mathrm{2}{h}}\left[{t}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }+\mathrm{ln}\:\left({t}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right)\right]_{\mathrm{0}} ^{\frac{\mathrm{2}{h}}{{b}}} \\ $$$$=\frac{{b}^{\mathrm{2}} }{\mathrm{2}{h}}\left\{\left(\frac{\mathrm{2}{h}}{{b}}\right)\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{h}}{{b}}\right)^{\mathrm{2}} }+\mathrm{ln}\:\left[\left(\frac{\mathrm{2}{h}}{{b}}\right)+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{h}}{{b}}\right)^{\mathrm{2}} }\right]\right\} \\ $$$$=\frac{\mathrm{2}{h}}{\left(\frac{\mathrm{2}{h}}{{b}}\right)^{\mathrm{2}} }\left\{\left(\frac{\mathrm{2}{h}}{{b}}\right)\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{h}}{{b}}\right)^{\mathrm{2}} }+\mathrm{ln}\:\left[\left(\frac{\mathrm{2}{h}}{{b}}\right)+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{h}}{{b}}\right)^{\mathrm{2}} }\right]\right\} \\ $$$${let}\:\alpha=\frac{\mathrm{2}{h}}{{b}} \\ $$$${L}=\frac{\mathrm{2}{h}}{\alpha^{\mathrm{2}} }\left[\alpha\sqrt{\mathrm{1}+\alpha^{\mathrm{2}} }+\mathrm{ln}\:\left(\alpha+\sqrt{\mathrm{1}+\alpha^{\mathrm{2}} }\right)\right] \\ $$$${since}\:{h}=\mathrm{7}.\mathrm{5}\:{and}\:{L}=\mathrm{25} \\ $$$$\frac{\mathrm{15}}{\alpha^{\mathrm{2}} }\left[\alpha\sqrt{\mathrm{1}+\alpha^{\mathrm{2}} }+\mathrm{ln}\:\left(\alpha+\sqrt{\mathrm{1}+\alpha^{\mathrm{2}} }\right)\right]=\mathrm{25} \\ $$$$\alpha\sqrt{\mathrm{1}+\alpha^{\mathrm{2}} }+\mathrm{ln}\:\left(\alpha+\sqrt{\mathrm{1}+\alpha^{\mathrm{2}} }\right)−\frac{\mathrm{25}}{\mathrm{15}}\alpha^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\alpha\approx\mathrm{1}.\mathrm{6} \\ $$$$\Rightarrow{Distance}\:{l}=\mathrm{2}{b}=\frac{\mathrm{4}{h}}{\alpha}=\frac{\mathrm{4}×\mathrm{7}.\mathrm{5}}{\mathrm{1}.\mathrm{6}}=\mathrm{18}.\mathrm{75}\:{m} \\ $$
Commented by mrW1 last updated on 22/Apr/17

