Question Number 12623 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 27/Apr/17
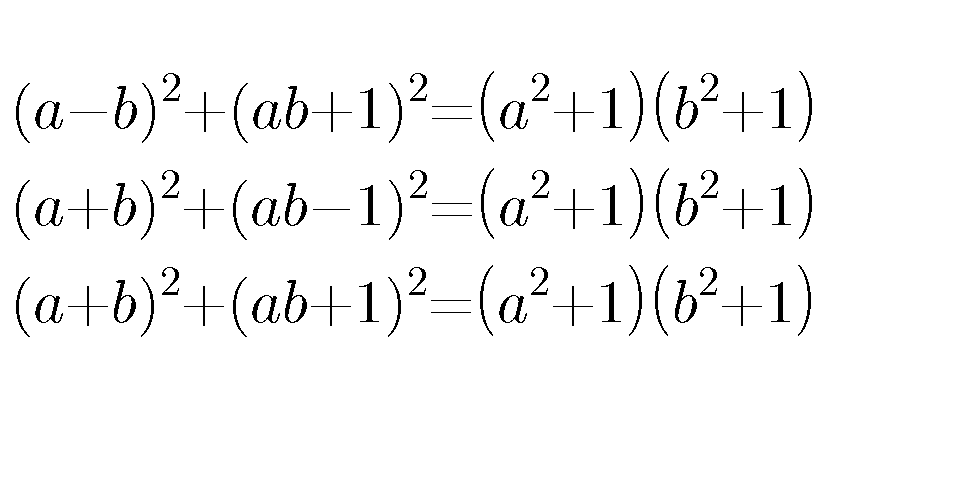
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 27/Apr/17
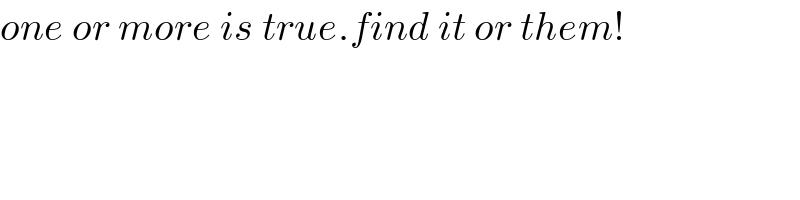
$${one}\:{or}\:{more}\:{is}\:{true}.{find}\:{it}\:{or}\:{them}! \\ $$
Answered by prakash jain last updated on 27/Apr/17
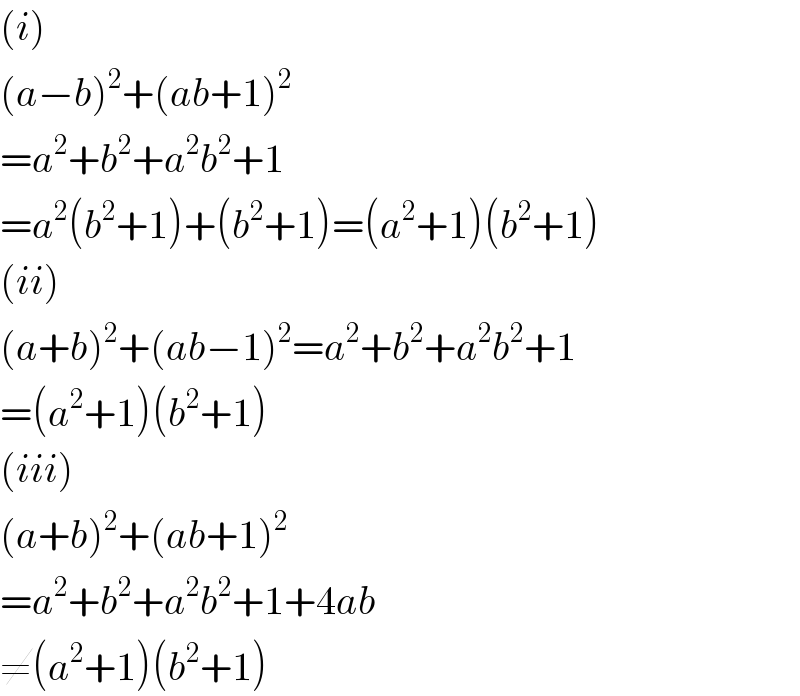
$$\left({i}\right) \\ $$$$\left({a}−{b}\right)^{\mathrm{2}} +\left({ab}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{a}^{\mathrm{2}} {b}^{\mathrm{2}} +\mathrm{1} \\ $$$$={a}^{\mathrm{2}} \left({b}^{\mathrm{2}} +\mathrm{1}\right)+\left({b}^{\mathrm{2}} +\mathrm{1}\right)=\left({a}^{\mathrm{2}} +\mathrm{1}\right)\left({b}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\left({ii}\right) \\ $$$$\left({a}+{b}\right)^{\mathrm{2}} +\left({ab}−\mathrm{1}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{a}^{\mathrm{2}} {b}^{\mathrm{2}} +\mathrm{1} \\ $$$$=\left({a}^{\mathrm{2}} +\mathrm{1}\right)\left({b}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\left({iii}\right) \\ $$$$\left({a}+{b}\right)^{\mathrm{2}} +\left({ab}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{a}^{\mathrm{2}} {b}^{\mathrm{2}} +\mathrm{1}+\mathrm{4}{ab} \\ $$$$\neq\left({a}^{\mathrm{2}} +\mathrm{1}\right)\left({b}^{\mathrm{2}} +\mathrm{1}\right) \\ $$
