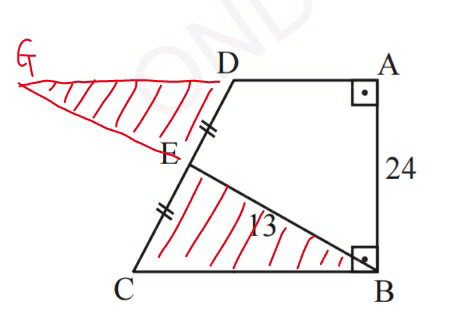
Question Number 12628 by sin (x) last updated on 27/Apr/17
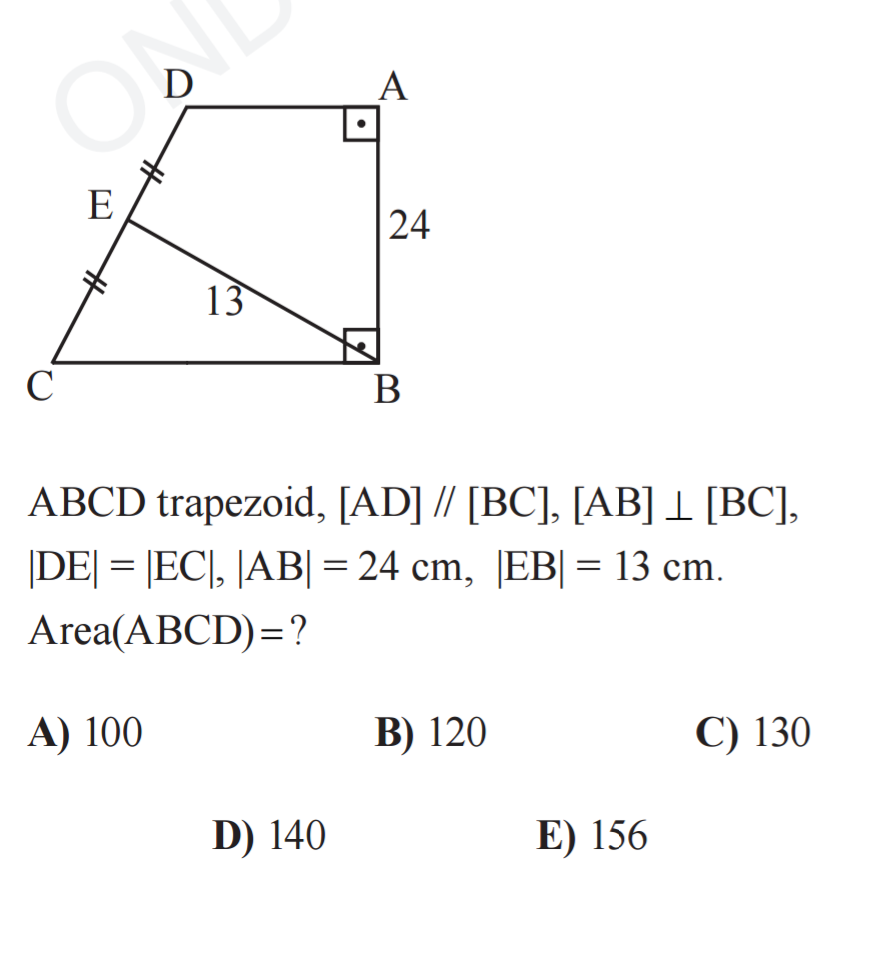
Answered by ajfour last updated on 27/Apr/17
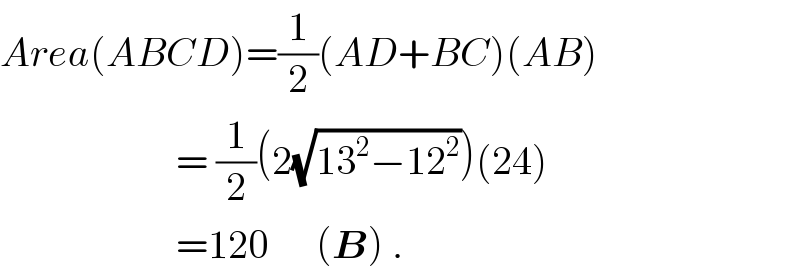
$${Area}\left({ABCD}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({AD}+{BC}\right)\left({AB}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}\sqrt{\mathrm{13}^{\mathrm{2}} −\mathrm{12}^{\mathrm{2}} }\right)\left(\mathrm{24}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{120}\:\:\:\:\:\:\left(\boldsymbol{{B}}\right)\:. \\ $$
Commented by Joel577 last updated on 28/Apr/17

$$\mathrm{please}\:\mathrm{explain}\:\mathrm{sir} \\ $$
Commented by mrW1 last updated on 28/Apr/17
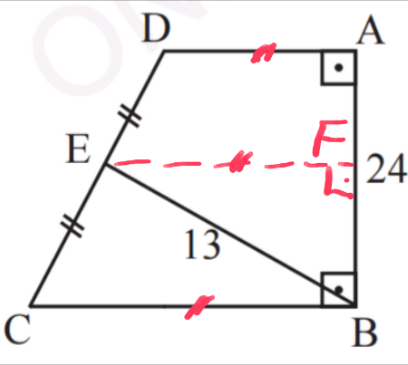
Answered by mrW1 last updated on 28/Apr/17
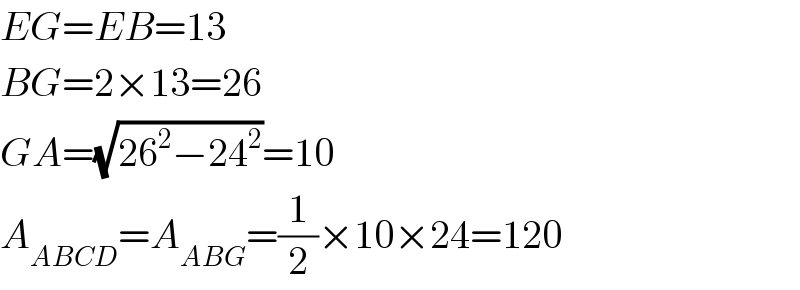
$${EG}={EB}=\mathrm{13} \\ $$$${BG}=\mathrm{2}×\mathrm{13}=\mathrm{26} \\ $$$${GA}=\sqrt{\mathrm{26}^{\mathrm{2}} −\mathrm{24}^{\mathrm{2}} }=\mathrm{10} \\ $$$${A}_{{ABCD}} ={A}_{{ABG}} =\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{10}×\mathrm{24}=\mathrm{120} \\ $$
Commented by mrW1 last updated on 29/Apr/17