Question-12635

Question Number 12635 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 27/Apr/17

Answered by mrW1 last updated on 27/Apr/17

x^2 −2xtan ϕ−1 =x^2 −2xtan ϕ+tan^2 ϕ−1−tan^2 ϕ =(x−tan ϕ)^2 −cosec^2 ϕ =(x−tan ϕ+cosec ϕ)(x−tan ϕ−cosec ϕ) (1/(x^2 −2xtan ϕ−1))=((cos ϕ)/2)((1/(x−tan ϕ−cosec ϕ))−(1/(x−tan ϕ+cosec ϕ))) ∫(dx/(x^2 −2xtan ϕ−1))=((cos ϕ)/2)∫((1/(x−tan ϕ−cosec ϕ))−(1/(x−tan ϕ+cosec ϕ)))dx =((cos ϕ)/2)×ln∣ ((x−tan ϕ−cosec ϕ)/(x−tan ϕ+cosec ϕ))∣+C =((cos ϕ)/2)×ln∣ ((xcos ϕ−sin ϕ−1)/(xcos ϕ−sin ϕ+1))∣+C

$${x}^{\mathrm{2}} −\mathrm{2}{x}\mathrm{tan}\:\varphi−\mathrm{1} \\ $$$$={x}^{\mathrm{2}} −\mathrm{2}{x}\mathrm{tan}\:\varphi+\mathrm{tan}^{\mathrm{2}} \:\varphi−\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\varphi \\ $$$$=\left({x}−\mathrm{tan}\:\varphi\right)^{\mathrm{2}} −\mathrm{cosec}^{\mathrm{2}} \:\varphi \\ $$$$=\left({x}−\mathrm{tan}\:\varphi+\mathrm{cosec}\:\varphi\right)\left({x}−\mathrm{tan}\:\varphi−\mathrm{cosec}\:\varphi\right) \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{2}{x}\mathrm{tan}\:\varphi−\mathrm{1}}=\frac{\mathrm{cos}\:\varphi}{\mathrm{2}}\left(\frac{\mathrm{1}}{{x}−\mathrm{tan}\:\varphi−\mathrm{cosec}\:\varphi}−\frac{\mathrm{1}}{{x}−\mathrm{tan}\:\varphi+\mathrm{cosec}\:\varphi}\right) \\ $$$$\int\frac{{dx}}{{x}^{\mathrm{2}} −\mathrm{2}{x}\mathrm{tan}\:\varphi−\mathrm{1}}=\frac{\mathrm{cos}\:\varphi}{\mathrm{2}}\int\left(\frac{\mathrm{1}}{{x}−\mathrm{tan}\:\varphi−\mathrm{cosec}\:\varphi}−\frac{\mathrm{1}}{{x}−\mathrm{tan}\:\varphi+\mathrm{cosec}\:\varphi}\right){dx} \\ $$$$=\frac{\mathrm{cos}\:\varphi}{\mathrm{2}}×\mathrm{ln}\mid\:\frac{{x}−\mathrm{tan}\:\varphi−\mathrm{cosec}\:\varphi}{{x}−\mathrm{tan}\:\varphi+\mathrm{cosec}\:\varphi}\mid+{C} \\ $$$$=\frac{\mathrm{cos}\:\varphi}{\mathrm{2}}×\mathrm{ln}\mid\:\frac{{x}\mathrm{cos}\:\varphi−\mathrm{sin}\:\varphi−\mathrm{1}}{{x}\mathrm{cos}\:\varphi−\mathrm{sin}\:\varphi+\mathrm{1}}\mid+{C} \\ $$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 27/Apr/17

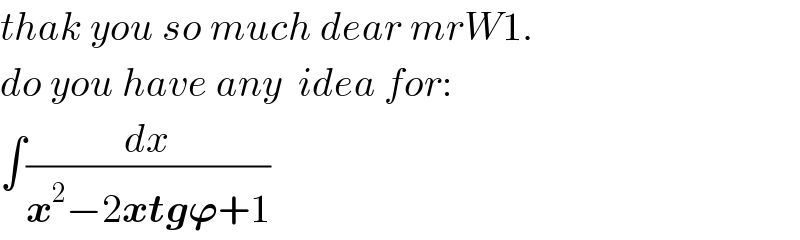
thak you so much dear mrW1. do you have any idea for: ∫(dx/(x^2 −2xtg𝛟+1))

$${thak}\:{you}\:{so}\:{much}\:{dear}\:{mrW}\mathrm{1}. \\ $$$${do}\:{you}\:{have}\:{any}\:\:{idea}\:{for}: \\ $$$$\int\frac{{dx}}{\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{xtg}\varphi}+\mathrm{1}} \\ $$

Commented by mrW1 last updated on 27/Apr/17

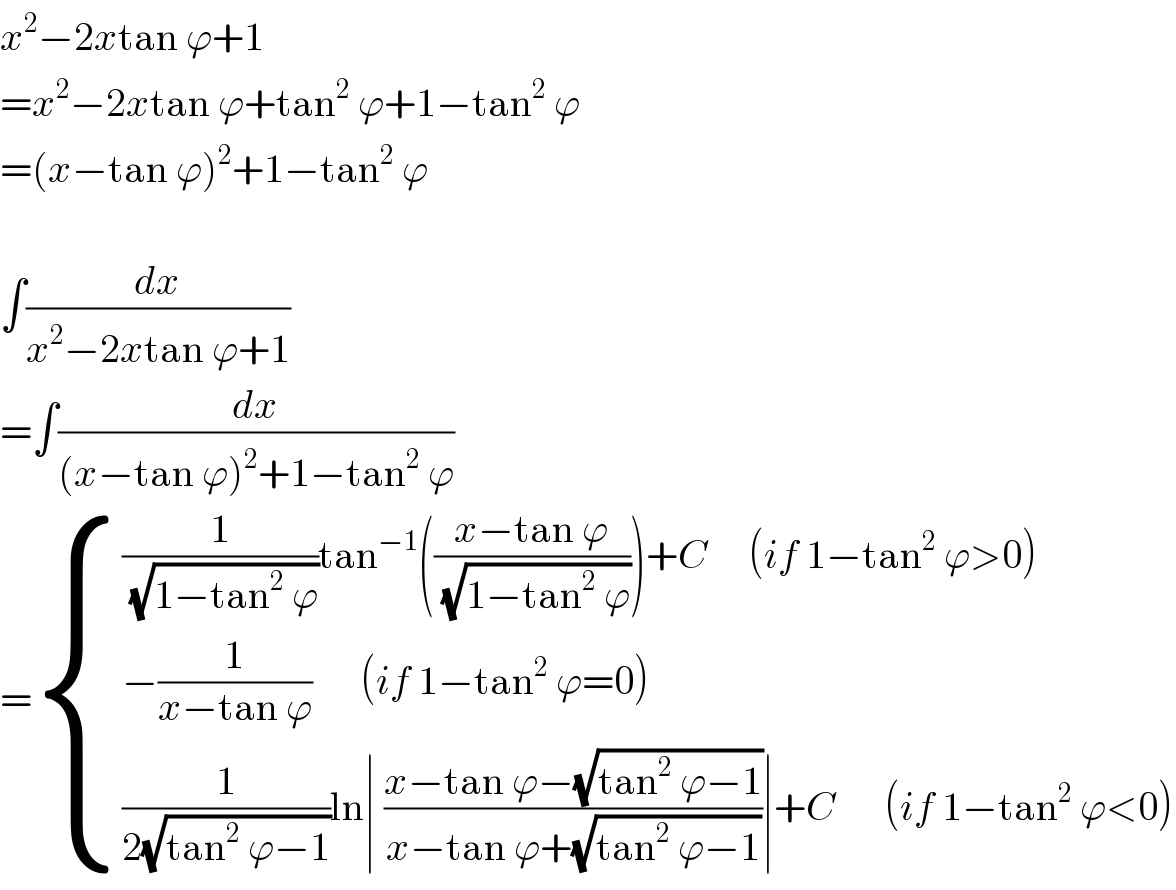
x^2 −2xtan ϕ+1 =x^2 −2xtan ϕ+tan^2 ϕ+1−tan^2 ϕ =(x−tan ϕ)^2 +1−tan^2 ϕ ∫(dx/(x^2 −2xtan ϕ+1)) =∫(dx/((x−tan ϕ)^2 +1−tan^2 ϕ)) = { (((1/( (√(1−tan^2 ϕ))))tan^(−1) (((x−tan ϕ)/( (√(1−tan^2 ϕ)))))+C (if 1−tan^2 ϕ>0))),((−(1/(x−tan ϕ)) (if 1−tan^2 ϕ=0))),(((1/(2(√(tan^2 ϕ−1))))ln∣ ((x−tan ϕ−(√(tan^2 ϕ−1)))/(x−tan ϕ+(√(tan^2 ϕ−1))))∣+C (if 1−tan^2 ϕ<0))) :}

$${x}^{\mathrm{2}} −\mathrm{2}{x}\mathrm{tan}\:\varphi+\mathrm{1} \\ $$$$={x}^{\mathrm{2}} −\mathrm{2}{x}\mathrm{tan}\:\varphi+\mathrm{tan}^{\mathrm{2}} \:\varphi+\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\varphi \\ $$$$=\left({x}−\mathrm{tan}\:\varphi\right)^{\mathrm{2}} +\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\varphi \\ $$$$ \\ $$$$\int\frac{{dx}}{{x}^{\mathrm{2}} −\mathrm{2}{x}\mathrm{tan}\:\varphi+\mathrm{1}} \\ $$$$=\int\frac{{dx}}{\left({x}−\mathrm{tan}\:\varphi\right)^{\mathrm{2}} +\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\varphi} \\ $$$$=\begin{cases}{\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\varphi}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}−\mathrm{tan}\:\varphi}{\:\sqrt{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\varphi}}\right)+{C}\:\:\:\:\:\left({if}\:\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\varphi>\mathrm{0}\right)}\\{−\frac{\mathrm{1}}{{x}−\mathrm{tan}\:\varphi}\:\:\:\:\:\:\left({if}\:\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\varphi=\mathrm{0}\right)}\\{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{tan}^{\mathrm{2}} \:\varphi−\mathrm{1}}}\mathrm{ln}\mid\:\frac{{x}−\mathrm{tan}\:\varphi−\sqrt{\mathrm{tan}^{\mathrm{2}} \:\varphi−\mathrm{1}}}{{x}−\mathrm{tan}\:\varphi+\sqrt{\mathrm{tan}^{\mathrm{2}} \:\varphi−\mathrm{1}}}\mid+{C}\:\:\:\:\:\:\left({if}\:\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\varphi<\mathrm{0}\right)}\end{cases} \\ $$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 27/Apr/17