Question-12684

Question Number 12684 by tawa last updated on 29/Apr/17

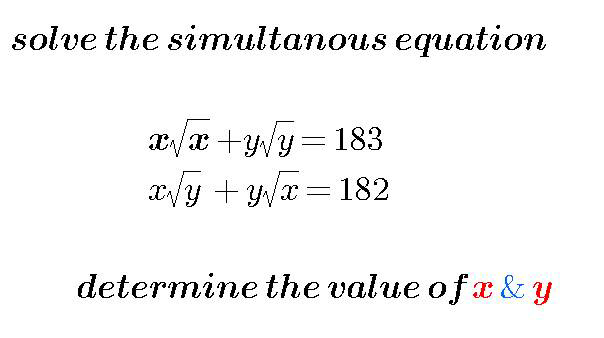
Answered by mrW1 last updated on 29/Apr/17

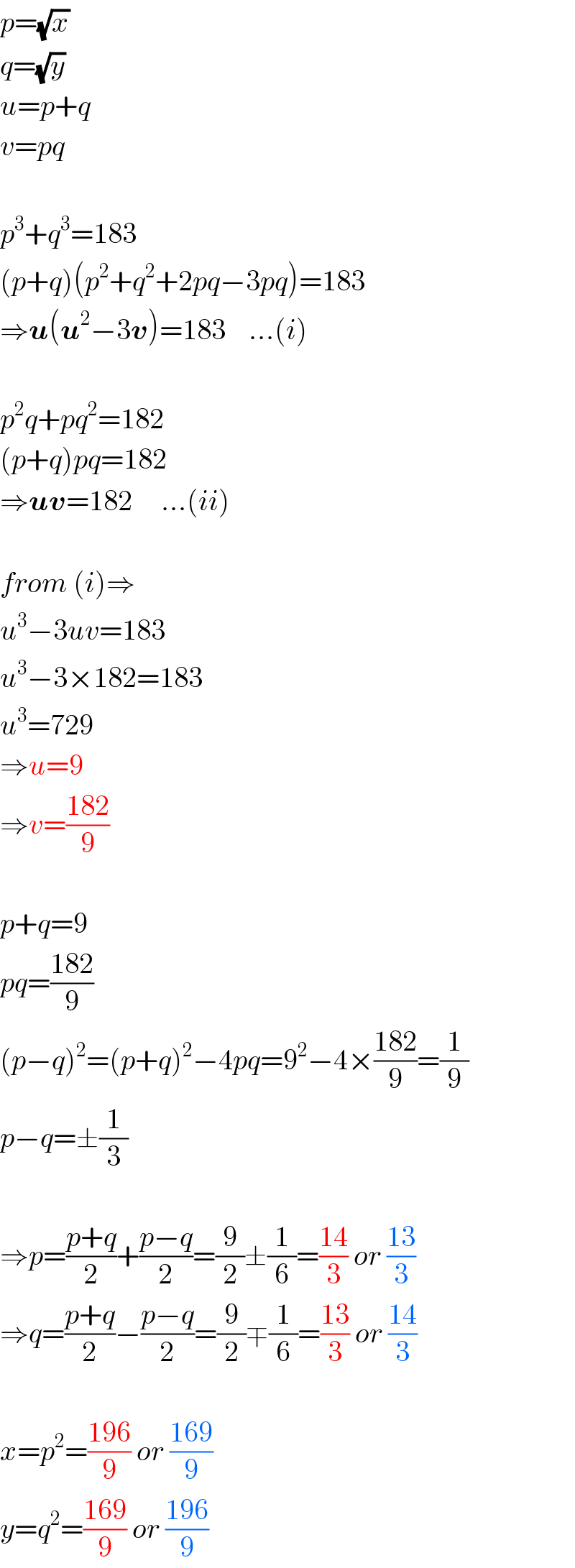
p=(√x) q=(√y) u=p+q v=pq p^3 +q^3 =183 (p+q)(p^2 +q^2 +2pq−3pq)=183 ⇒u(u^2 −3v)=183 ...(i) p^2 q+pq^2 =182 (p+q)pq=182 ⇒uv=182 ...(ii) from (i)⇒ u^3 −3uv=183 u^3 −3×182=183 u^3 =729 ⇒u=9 ⇒v=((182)/9) p+q=9 pq=((182)/9) (p−q)^2 =(p+q)^2 −4pq=9^2 −4×((182)/9)=(1/9) p−q=±(1/3) ⇒p=((p+q)/2)+((p−q)/2)=(9/2)±(1/6)=((14)/3) or ((13)/3) ⇒q=((p+q)/2)−((p−q)/2)=(9/2)∓(1/6)=((13)/3) or ((14)/3) x=p^2 =((196)/9) or ((169)/9) y=q^2 =((169)/9) or ((196)/9)

$${p}=\sqrt{{x}} \\ $$$${q}=\sqrt{{y}} \\ $$$${u}={p}+{q} \\ $$$${v}={pq} \\ $$$$ \\ $$$${p}^{\mathrm{3}} +{q}^{\mathrm{3}} =\mathrm{183} \\ $$$$\left({p}+{q}\right)\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +\mathrm{2}{pq}−\mathrm{3}{pq}\right)=\mathrm{183} \\ $$$$\Rightarrow\boldsymbol{{u}}\left(\boldsymbol{{u}}^{\mathrm{2}} −\mathrm{3}\boldsymbol{{v}}\right)=\mathrm{183}\:\:\:\:…\left({i}\right) \\ $$$$ \\ $$$${p}^{\mathrm{2}} {q}+{pq}^{\mathrm{2}} =\mathrm{182} \\ $$$$\left({p}+{q}\right){pq}=\mathrm{182} \\ $$$$\Rightarrow\boldsymbol{{uv}}=\mathrm{182}\:\:\:\:\:…\left({ii}\right) \\ $$$$ \\ $$$${from}\:\left({i}\right)\Rightarrow \\ $$$${u}^{\mathrm{3}} −\mathrm{3}{uv}=\mathrm{183} \\ $$$${u}^{\mathrm{3}} −\mathrm{3}×\mathrm{182}=\mathrm{183} \\ $$$${u}^{\mathrm{3}} =\mathrm{729} \\ $$$$\Rightarrow{u}=\mathrm{9} \\ $$$$\Rightarrow{v}=\frac{\mathrm{182}}{\mathrm{9}} \\ $$$$ \\ $$$${p}+{q}=\mathrm{9} \\ $$$${pq}=\frac{\mathrm{182}}{\mathrm{9}} \\ $$$$\left({p}−{q}\right)^{\mathrm{2}} =\left({p}+{q}\right)^{\mathrm{2}} −\mathrm{4}{pq}=\mathrm{9}^{\mathrm{2}} −\mathrm{4}×\frac{\mathrm{182}}{\mathrm{9}}=\frac{\mathrm{1}}{\mathrm{9}} \\ $$$${p}−{q}=\pm\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$ \\ $$$$\Rightarrow{p}=\frac{{p}+{q}}{\mathrm{2}}+\frac{{p}−{q}}{\mathrm{2}}=\frac{\mathrm{9}}{\mathrm{2}}\pm\frac{\mathrm{1}}{\mathrm{6}}=\frac{\mathrm{14}}{\mathrm{3}}\:{or}\:\frac{\mathrm{13}}{\mathrm{3}} \\ $$$$\Rightarrow{q}=\frac{{p}+{q}}{\mathrm{2}}−\frac{{p}−{q}}{\mathrm{2}}=\frac{\mathrm{9}}{\mathrm{2}}\mp\frac{\mathrm{1}}{\mathrm{6}}=\frac{\mathrm{13}}{\mathrm{3}}\:{or}\:\frac{\mathrm{14}}{\mathrm{3}} \\ $$$$ \\ $$$${x}={p}^{\mathrm{2}} =\frac{\mathrm{196}}{\mathrm{9}}\:{or}\:\frac{\mathrm{169}}{\mathrm{9}} \\ $$$${y}={q}^{\mathrm{2}} =\frac{\mathrm{169}}{\mathrm{9}}\:{or}\:\frac{\mathrm{196}}{\mathrm{9}} \\ $$

Commented by tawa last updated on 29/Apr/17

$$\mathrm{wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply