Menu Close

Question-12725

Tinku Tara 0 Comments
Pin




Question Number 12725 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 29/Apr/17
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 29/Apr/17
in triangle: ABC,point D located on triangle plan,such that: ∠ADB=∠BDC=∠CDA and: DH∥AB ,DG∥BC ,DF∥AC. 1)find: ((DH)/(AB))+((DG)/(BC))+((DF)/(AC)) . 2)prove: DH+DG+DF<DA+DB+DC 3)(S_(ADG) /S_(DBH) )=?
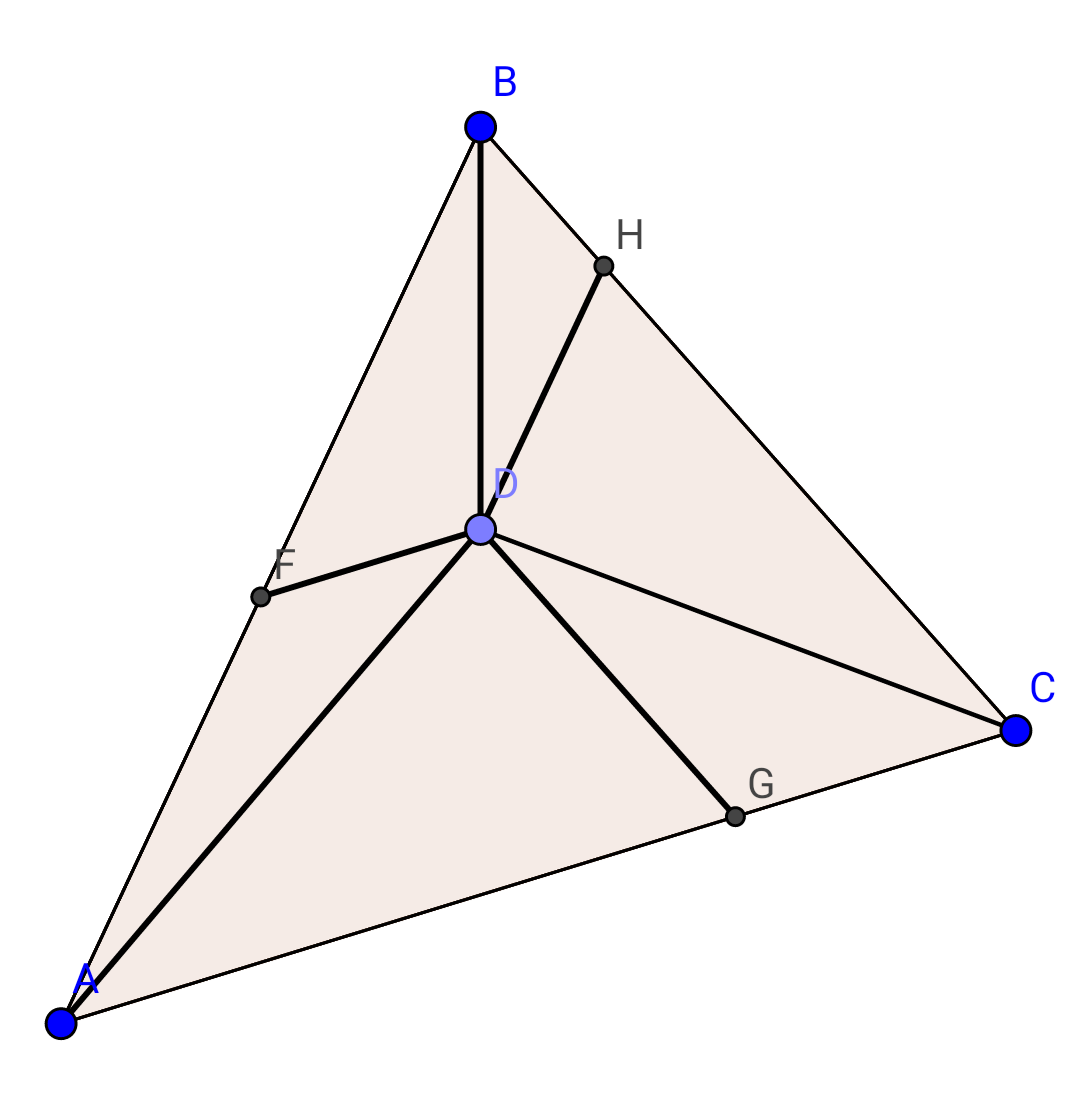
$${in}\:{triangle}:\:{ABC},{point}\:\:{D}\:{located}\:{on} \\ $$$${triangle}\:{plan},{such}\:{that}: \\ $$$$\angle{ADB}=\angle{BDC}=\angle{CDA}\:{and}: \\ $$$${DH}\parallel{AB}\:,{DG}\parallel{BC}\:,{DF}\parallel{AC}. \\ $$$$\left.\mathrm{1}\right){find}:\:\frac{{DH}}{{AB}}+\frac{{DG}}{{BC}}+\frac{{DF}}{{AC}}\:. \\ $$$$\left.\mathrm{2}\right){prove}:\:{DH}+{DG}+{DF}<{DA}+{DB}+{DC} \\ $$$$\left.\mathrm{3}\right)\frac{{S}_{{ADG}} }{{S}_{{DBH}} }=? \\ $$
Commented by mrW1 last updated on 01/May/17
Commented by mrW1 last updated on 01/May/17
what do you mean in question 3?
$${what}\:{do}\:{you}\:{mean}\:{in}\:{question}\:\mathrm{3}? \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 01/May/17
hello dear mrW1.thank you so much for solving this question.you are number one in tinku tara. about your communet: S_(ADG) = area of triangle ADG and so.
$${hello}\:{dear}\:{mrW}\mathrm{1}.{thank}\:{you}\:{so}\:{much} \\ $$$${for}\:{solving}\:{this}\:{question}.{you}\:{are}\: \\ $$$${number}\:{one}\:{in}\:{tinku}\:{tara}. \\ $$$${about}\:{your}\:{communet}: \\ $$$${S}_{{ADG}} =\:{area}\:{of}\:{triangle}\:{ADG}\:{and}\:{so}. \\ $$
Answered by mrW1 last updated on 01/May/17
Question 1) since ∡ADB=∡ADC=∡BDC ⇒ ∡ADB=∡ADC=∡BDC=((360)/3)=120° sin 120°=((√3)/2) cos 120°=−(1/2) let DA^(−) =a let DB^(−) =b let DC^(−) =c AC^2 =a^2 +c^2 −2ac×cos ∡ADC=a^2 +c^2 +ac ⇒AC=(√(a^2 +c^2 +ac)) similarily ⇒AB=(√(a^2 +b^2 +ab)) ⇒BC=(√(b^2 +c^2 +bc)) in ΔBDC: ((BC)/(sin 120°))=(b/(sin β))=(c/(sin (60−β))) ...(i) in ΔADC: ((AC)/(sin 120°))=(a/(sin α))=(c/(sin (60−α))) ...(ii) from (i): (c/b)sin β=sin (60−β)=sin 60 cos β−cos 60 sin β (c/b)sin β=((√3)/2)cos β−(1/2) sin β ⇒cos β=((2c+b)/( (√3)b)) sin β similarily from (ii): ⇒cos α=((2c+a)/( (√3)a)) sin α sin (α+β)=sin α cos β+sin β cos α =sin α ×((2c+b)/( (√3)b)) sin β+sin β ×((2c+a)/( (√3)a)) sin α =(2/( (√3)))×((ab+bc+ca)/(ab))×sin α sin β in ΔCDG: ((DG)/(sin α))=((DC)/(sin ∠CGD))=(c/(sin (180−α−β)))=(c/(sin (α+β))) ⇒DG=c×((sin α)/(sin (α+β)))=((c×sin α)/((2/( (√3)))×((ab+bc+ca)/(ab))×sin α sin β)) =((√3)/2)×(b/(sin β))×((ac)/(ab+bc+ca)) from (i) we have (b/(sin β))=((BC)/(sin 120°))=((BC)/((√3)/2)) ⇒((√3)/2)×(b/(sin β))=BC ⇒DG=BC×((ac)/(ab+bc+ca)) or ((DG)/(BC))=((ac)/(ab+bc+ca)) similarily ((DH)/(AB))=((bc)/(ab+bc+ca)) ((DF)/(AC))=((ab)/(ab+bc+ca)) ((DH)/(AB))+((DF)/(AC))+((DG)/(BC))=((bc+ab+ac)/(ab+bc+ca))=1
$$\left.\boldsymbol{{Question}}\:\mathrm{1}\right) \\ $$$$ \\ $$$${since}\:\measuredangle{ADB}=\measuredangle{ADC}=\measuredangle{BDC} \\ $$$$\Rightarrow\:\measuredangle{ADB}=\measuredangle{ADC}=\measuredangle{BDC}=\frac{\mathrm{360}}{\mathrm{3}}=\mathrm{120}° \\ $$$$\mathrm{sin}\:\mathrm{120}°=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\mathrm{cos}\:\mathrm{120}°=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$${let}\:\overline {{DA}}={a} \\ $$$${let}\:\overline {{DB}}={b} \\ $$$${let}\:\overline {{DC}}={c} \\ $$$$ \\ $$$${AC}^{\mathrm{2}} ={a}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{ac}×\mathrm{cos}\:\measuredangle{ADC}={a}^{\mathrm{2}} +{c}^{\mathrm{2}} +{ac} \\ $$$$\Rightarrow{AC}=\sqrt{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} +{ac}} \\ $$$${similarily} \\ $$$$\Rightarrow{AB}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{ab}} \\ $$$$\Rightarrow{BC}=\sqrt{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{bc}} \\ $$$$ \\ $$$${in}\:\Delta{BDC}: \\ $$$$\frac{{BC}}{\mathrm{sin}\:\mathrm{120}°}=\frac{{b}}{\mathrm{sin}\:\beta}=\frac{{c}}{\mathrm{sin}\:\left(\mathrm{60}−\beta\right)}\:\:\:\:…\left({i}\right) \\ $$$$ \\ $$$${in}\:\Delta{ADC}: \\ $$$$\frac{{AC}}{\mathrm{sin}\:\mathrm{120}°}=\frac{{a}}{\mathrm{sin}\:\alpha}=\frac{{c}}{\mathrm{sin}\:\left(\mathrm{60}−\alpha\right)}\:\:\:\:…\left({ii}\right) \\ $$$$ \\ $$$${from}\:\left({i}\right): \\ $$$$\frac{{c}}{{b}}\mathrm{sin}\:\beta=\mathrm{sin}\:\left(\mathrm{60}−\beta\right)=\mathrm{sin}\:\mathrm{60}\:\mathrm{cos}\:\beta−\mathrm{cos}\:\mathrm{60}\:\mathrm{sin}\:\beta \\ $$$$\frac{{c}}{{b}}\mathrm{sin}\:\beta=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{cos}\:\beta−\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{sin}\:\beta \\ $$$$\Rightarrow\mathrm{cos}\:\beta=\frac{\mathrm{2}{c}+{b}}{\:\sqrt{\mathrm{3}}{b}}\:\mathrm{sin}\:\beta \\ $$$${similarily}\:{from}\:\left({ii}\right): \\ $$$$\Rightarrow\mathrm{cos}\:\alpha=\frac{\mathrm{2}{c}+{a}}{\:\sqrt{\mathrm{3}}{a}}\:\mathrm{sin}\:\alpha \\ $$$$ \\ $$$$\mathrm{sin}\:\left(\alpha+\beta\right)=\mathrm{sin}\:\alpha\:\mathrm{cos}\:\beta+\mathrm{sin}\:\beta\:\mathrm{cos}\:\alpha \\ $$$$=\mathrm{sin}\:\alpha\:×\frac{\mathrm{2}{c}+{b}}{\:\sqrt{\mathrm{3}}{b}}\:\mathrm{sin}\:\beta+\mathrm{sin}\:\beta\:×\frac{\mathrm{2}{c}+{a}}{\:\sqrt{\mathrm{3}}{a}}\:\mathrm{sin}\:\alpha \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}×\frac{{ab}+{bc}+{ca}}{{ab}}×\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta \\ $$$$ \\ $$$${in}\:\Delta{CDG}: \\ $$$$\frac{{DG}}{\mathrm{sin}\:\alpha}=\frac{{DC}}{\mathrm{sin}\:\angle{CGD}}=\frac{{c}}{\mathrm{sin}\:\left(\mathrm{180}−\alpha−\beta\right)}=\frac{{c}}{\mathrm{sin}\:\left(\alpha+\beta\right)} \\ $$$$\Rightarrow{DG}={c}×\frac{\mathrm{sin}\:\alpha}{\mathrm{sin}\:\left(\alpha+\beta\right)}=\frac{{c}×\mathrm{sin}\:\alpha}{\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}×\frac{{ab}+{bc}+{ca}}{{ab}}×\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta} \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×\frac{{b}}{\mathrm{sin}\:\beta}×\frac{{ac}}{{ab}+{bc}+{ca}} \\ $$$$ \\ $$$${from}\:\left({i}\right)\:{we}\:{have} \\ $$$$\frac{{b}}{\mathrm{sin}\:\beta}=\frac{{BC}}{\mathrm{sin}\:\mathrm{120}°}=\frac{{BC}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \\ $$$$\Rightarrow\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×\frac{{b}}{\mathrm{sin}\:\beta}={BC} \\ $$$$ \\ $$$$\Rightarrow{DG}={BC}×\frac{{ac}}{{ab}+{bc}+{ca}} \\ $$$${or} \\ $$$$\frac{{DG}}{{BC}}=\frac{{ac}}{{ab}+{bc}+{ca}} \\ $$$$ \\ $$$${similarily} \\ $$$$\frac{{DH}}{{AB}}=\frac{{bc}}{{ab}+{bc}+{ca}} \\ $$$$\frac{{DF}}{{AC}}=\frac{{ab}}{{ab}+{bc}+{ca}} \\ $$$$ \\ $$$$\frac{{DH}}{{AB}}+\frac{{DF}}{{AC}}+\frac{{DG}}{{BC}}=\frac{{bc}+{ab}+{ac}}{{ab}+{bc}+{ca}}=\mathrm{1} \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 01/May/17
so beautiful .thanks a lot.
$${so}\:{beautiful}\:.{thanks}\:{a}\:{lot}. \\ $$
Answered by mrW1 last updated on 01/May/17
Question 2) see above: DG=((ac)/(ab+bc+ca))×BC =((ac)/(ab+bc+ca))×(√(b^2 +c^2 +bc)) <((ac)/(ab+bc+ca))×(√(b^2 +c^2 +2bc)) =((ac(b+c))/(ab+bc+ca)) ⇒DG<((ac(b+c))/(ab+bc+ca)) similarily DH<((bc(a+b))/(ab+bc+ca)) DF<((ab(c+a))/(ab+bc+ca)) DG+DH+DF<((ac(b+c)+bc(a+b)+ab(c+a))/(ab+bc+ca)) =((ac(a+b+c)+bc(a+b+c)+ab(c+a+b)−a^2 c−c^2 b−b^2 a)/(ab+bc+ca)) =(((ac+bc+ab)(a+b+c)−a^2 c−c^2 b−b^2 a)/(ab+bc+ca)) =a+b+c−((a^2 c+c^2 b+b^2 a)/(ab+bc+ca)) <a+b+c =DA+DB+DC
$$\left.\boldsymbol{{Question}}\:\mathrm{2}\right) \\ $$$$ \\ $$$${see}\:{above}: \\ $$$${DG}=\frac{{ac}}{{ab}+{bc}+{ca}}×{BC} \\ $$$$=\frac{{ac}}{{ab}+{bc}+{ca}}×\sqrt{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{bc}} \\ $$$$<\frac{{ac}}{{ab}+{bc}+{ca}}×\sqrt{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{2}{bc}} \\ $$$$=\frac{{ac}\left({b}+{c}\right)}{{ab}+{bc}+{ca}} \\ $$$$\Rightarrow{DG}<\frac{{ac}\left({b}+{c}\right)}{{ab}+{bc}+{ca}} \\ $$$$ \\ $$$${similarily} \\ $$$${DH}<\frac{{bc}\left({a}+{b}\right)}{{ab}+{bc}+{ca}} \\ $$$${DF}<\frac{{ab}\left({c}+{a}\right)}{{ab}+{bc}+{ca}} \\ $$$$ \\ $$$${DG}+{DH}+{DF}<\frac{{ac}\left({b}+{c}\right)+{bc}\left({a}+{b}\right)+{ab}\left({c}+{a}\right)}{{ab}+{bc}+{ca}} \\ $$$$=\frac{{ac}\left({a}+{b}+{c}\right)+{bc}\left({a}+{b}+{c}\right)+{ab}\left({c}+{a}+{b}\right)−{a}^{\mathrm{2}} {c}−{c}^{\mathrm{2}} {b}−{b}^{\mathrm{2}} {a}}{{ab}+{bc}+{ca}} \\ $$$$=\frac{\left({ac}+{bc}+{ab}\right)\left({a}+{b}+{c}\right)−{a}^{\mathrm{2}} {c}−{c}^{\mathrm{2}} {b}−{b}^{\mathrm{2}} {a}}{{ab}+{bc}+{ca}} \\ $$$$={a}+{b}+{c}−\frac{{a}^{\mathrm{2}} {c}+{c}^{\mathrm{2}} {b}+{b}^{\mathrm{2}} {a}}{{ab}+{bc}+{ca}} \\ $$$$<{a}+{b}+{c} \\ $$$$={DA}+{DB}+{DC} \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 01/May/17
perfect and nice.thank you very much.
$${perfect}\:{and}\:{nice}.{thank}\:{you}\:{very}\:{much}. \\ $$
Answered by mrW1 last updated on 01/May/17
Question 3) ((GC)/(AC))=((DH)/(AB))=((bc)/(ab+bc+ca)) S_(ΔADC) =(1/2)×ac×sin 120°=((√3)/4)ac S_(ΔGDC) =((GC)/(AC))×S_(ΔADC) =((bc)/(ab+bc+ca))×(((√3)ac)/4) S_(ΔADG) =(1−((GC)/(AC)))×S_(ΔADC) =(1−((bc)/(ab+bc+ca)))×(((√3)ac)/4)=(((√3)a^2 c(b+c))/(4(ab+bc+ca))) similarily S_(ΔBDH) =((DF)/(AC))×S_(ΔBDC) =((ab)/(ab+bc+ca))×(((√3)bc)/4)=(((√3)ab^2 c)/(4(ab+bc+ca))) ⇒(S_(ΔADG) /S_(ΔBDH) )=((a^2 c(b+c))/(ab^2 c))=((a(b+c))/b^2 )=(a/b)(1+(c/b))
$$\left.\boldsymbol{{Question}}\:\mathrm{3}\right) \\ $$$$ \\ $$$$\frac{{GC}}{{AC}}=\frac{{DH}}{{AB}}=\frac{{bc}}{{ab}+{bc}+{ca}} \\ $$$$ \\ $$$${S}_{\Delta{ADC}} =\frac{\mathrm{1}}{\mathrm{2}}×{ac}×\mathrm{sin}\:\mathrm{120}°=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}{ac} \\ $$$${S}_{\Delta{GDC}} =\frac{{GC}}{{AC}}×{S}_{\Delta{ADC}} =\frac{{bc}}{{ab}+{bc}+{ca}}×\frac{\sqrt{\mathrm{3}}{ac}}{\mathrm{4}} \\ $$$${S}_{\Delta{ADG}} =\left(\mathrm{1}−\frac{{GC}}{{AC}}\right)×{S}_{\Delta{ADC}} =\left(\mathrm{1}−\frac{{bc}}{{ab}+{bc}+{ca}}\right)×\frac{\sqrt{\mathrm{3}}{ac}}{\mathrm{4}}=\frac{\sqrt{\mathrm{3}}{a}^{\mathrm{2}} {c}\left({b}+{c}\right)}{\mathrm{4}\left({ab}+{bc}+{ca}\right)} \\ $$$$ \\ $$$${similarily} \\ $$$${S}_{\Delta{BDH}} =\frac{{DF}}{{AC}}×{S}_{\Delta{BDC}} =\frac{{ab}}{{ab}+{bc}+{ca}}×\frac{\sqrt{\mathrm{3}}{bc}}{\mathrm{4}}=\frac{\sqrt{\mathrm{3}}{ab}^{\mathrm{2}} {c}}{\mathrm{4}\left({ab}+{bc}+{ca}\right)} \\ $$$$ \\ $$$$\Rightarrow\frac{{S}_{\Delta{ADG}} }{{S}_{\Delta{BDH}} }=\frac{{a}^{\mathrm{2}} {c}\left({b}+{c}\right)}{{ab}^{\mathrm{2}} {c}}=\frac{{a}\left({b}+{c}\right)}{{b}^{\mathrm{2}} }=\frac{{a}}{{b}}\left(\mathrm{1}+\frac{{c}}{{b}}\right) \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 02/May/17
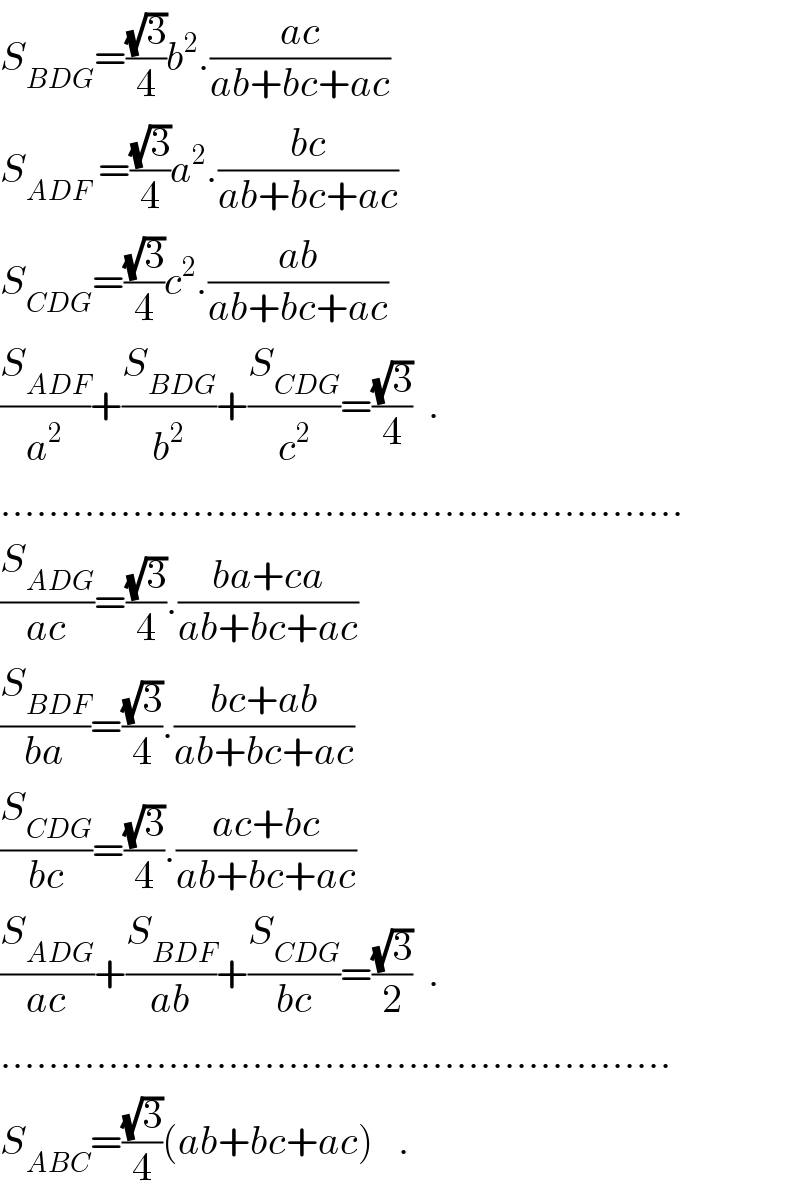
S_(BDG) =((√3)/4)b^2 .((ac)/(ab+bc+ac)) S_(ADF) =((√3)/4)a^2 .((bc)/(ab+bc+ac)) S_(CDG) =((√3)/4)c^2 .((ab)/(ab+bc+ac)) (S_(ADF) /a^2 )+(S_(BDG) /b^2 )+(S_(CDG) /c^2 )=((√3)/4) . ......................................................... (S_(ADG) /(ac))=((√3)/4).((ba+ca)/(ab+bc+ac)) (S_(BDF) /(ba))=((√3)/4).((bc+ab)/(ab+bc+ac)) (S_(CDG) /(bc))=((√3)/4).((ac+bc)/(ab+bc+ac)) (S_(ADG) /(ac))+(S_(BDF) /(ab))+(S_(CDG) /(bc))=((√3)/2) . ........................................................ S_(ABC) =((√3)/4)(ab+bc+ac) .
$${S}_{{BDG}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}{b}^{\mathrm{2}} .\frac{{ac}}{{ab}+{bc}+{ac}} \\ $$$${S}_{{ADF}} \:=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}{a}^{\mathrm{2}} .\frac{{bc}}{{ab}+{bc}+{ac}} \\ $$$${S}_{{CDG}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}{c}^{\mathrm{2}} .\frac{{ab}}{{ab}+{bc}+{ac}} \\ $$$$\frac{{S}_{{ADF}} }{{a}^{\mathrm{2}} }+\frac{{S}_{{BDG}} }{{b}^{\mathrm{2}} }+\frac{{S}_{{CDG}} }{{c}^{\mathrm{2}} }=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\:\:. \\ $$$$………………………………………………… \\ $$$$\frac{{S}_{{ADG}} }{{ac}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}.\frac{{ba}+{ca}}{{ab}+{bc}+{ac}} \\ $$$$\frac{{S}_{{BDF}} }{{ba}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}.\frac{{bc}+{ab}}{{ab}+{bc}+{ac}} \\ $$$$\frac{{S}_{{CDG}} }{{bc}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}.\frac{{ac}+{bc}}{{ab}+{bc}+{ac}} \\ $$$$\frac{{S}_{{ADG}} }{{ac}}+\frac{{S}_{{BDF}} }{{ab}}+\frac{{S}_{{CDG}} }{{bc}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:. \\ $$$$……………………………………………….. \\ $$$${S}_{{ABC}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\left({ab}+{bc}+{ac}\right)\:\:\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *