Question Number 12846 by Joel577 last updated on 04/May/17
Commented by Joel577 last updated on 04/May/17
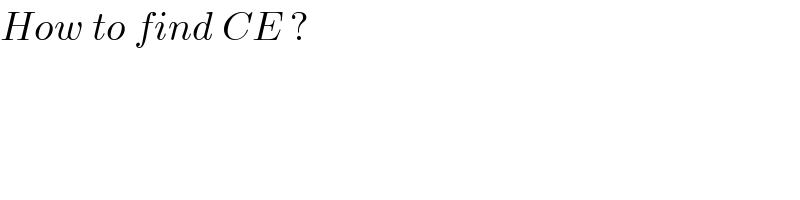
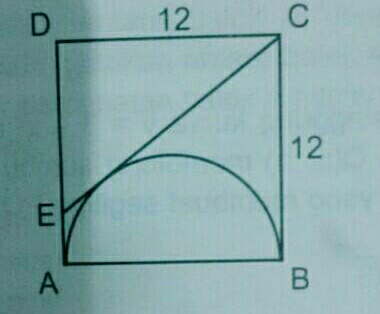
$${How}\:{to}\:{find}\:{CE}\:? \\ $$
Answered by mrW1 last updated on 04/May/17
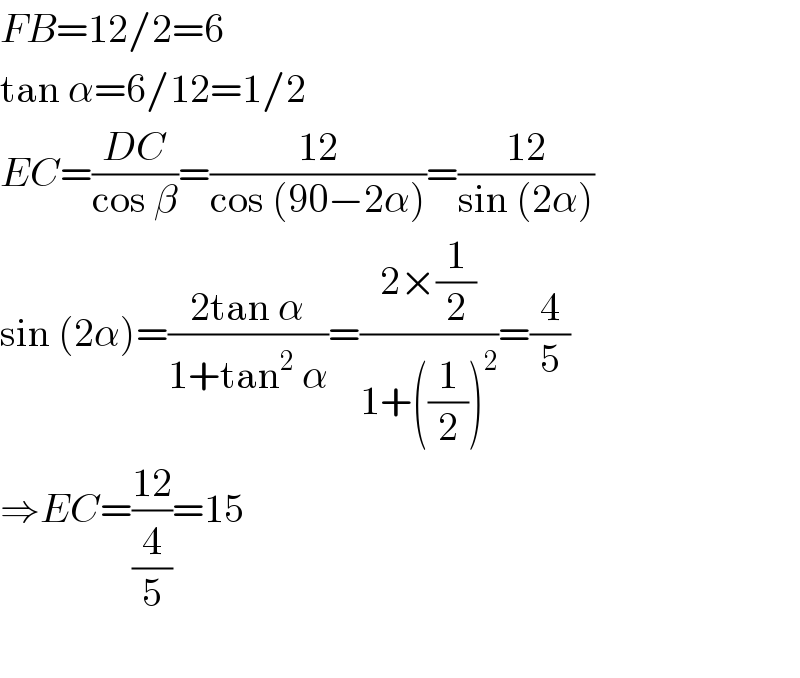
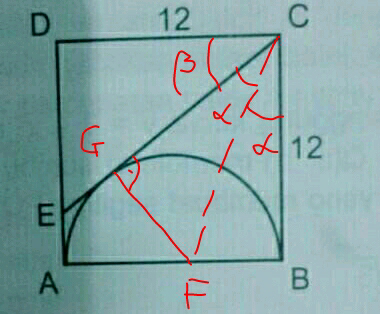
$${FB}=\mathrm{12}/\mathrm{2}=\mathrm{6} \\ $$$$\mathrm{tan}\:\alpha=\mathrm{6}/\mathrm{12}=\mathrm{1}/\mathrm{2} \\ $$$${EC}=\frac{{DC}}{\mathrm{cos}\:\beta}=\frac{\mathrm{12}}{\mathrm{cos}\:\left(\mathrm{90}−\mathrm{2}\alpha\right)}=\frac{\mathrm{12}}{\mathrm{sin}\:\left(\mathrm{2}\alpha\right)} \\ $$$$\mathrm{sin}\:\left(\mathrm{2}\alpha\right)=\frac{\mathrm{2tan}\:\alpha}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\alpha}=\frac{\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}+\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\Rightarrow{EC}=\frac{\mathrm{12}}{\frac{\mathrm{4}}{\mathrm{5}}}=\mathrm{15} \\ $$$$ \\ $$
Commented by mrW1 last updated on 04/May/17
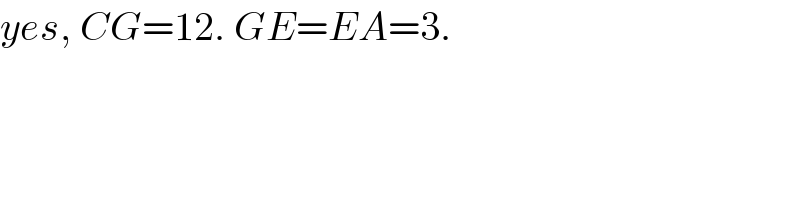
$${yes},\:{CG}=\mathrm{12}.\:{GE}={EA}=\mathrm{3}. \\ $$
Commented by mrW1 last updated on 04/May/17
Commented by Joel577 last updated on 04/May/17
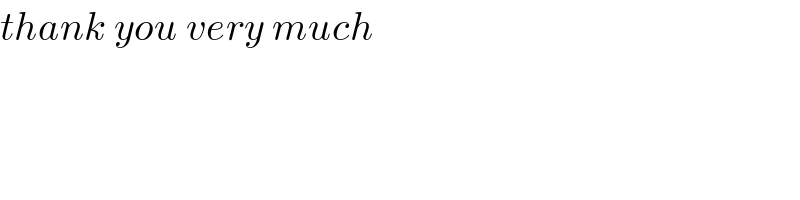
$${thank}\:{you}\:{very}\:{much} \\ $$
Commented by Joel577 last updated on 04/May/17
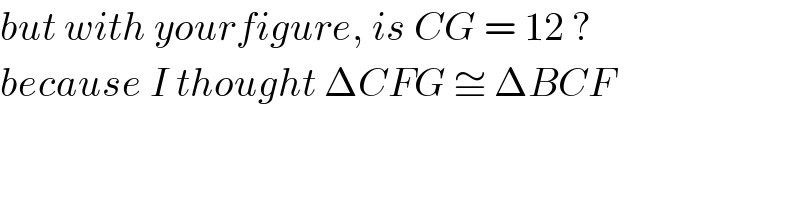
$${but}\:{with}\:{yourfigure},\:{is}\:{CG}\:=\:\mathrm{12}\:? \\ $$$${because}\:{I}\:{thought}\:\Delta{CFG}\:\cong\:\Delta{BCF} \\ $$
Commented by mrW1 last updated on 04/May/17
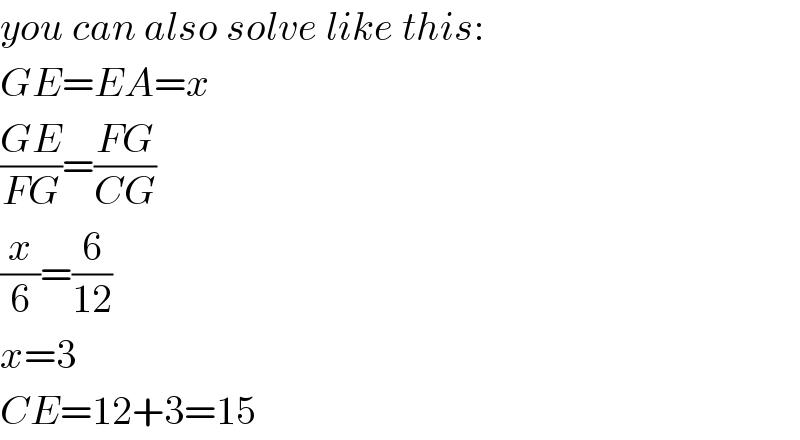
$${you}\:{can}\:{also}\:{solve}\:{like}\:{this}: \\ $$$${GE}={EA}={x} \\ $$$$\frac{{GE}}{{FG}}=\frac{{FG}}{{CG}} \\ $$$$\frac{{x}}{\mathrm{6}}=\frac{\mathrm{6}}{\mathrm{12}} \\ $$$${x}=\mathrm{3} \\ $$$${CE}=\mathrm{12}+\mathrm{3}=\mathrm{15} \\ $$
Commented by chux last updated on 04/May/17
$$\mathrm{wow}\:…..\mathrm{i}\:\mathrm{love}\:\mathrm{this} \\ $$$$ \\ $$
Commented by Joel577 last updated on 04/May/17
$${thank}\:{you}\:{very}\:{much} \\ $$
Commented by A Haq Soomro last updated on 06/May/17

$$\eta\overset{\bullet} {\imath}\subset\in! \\ $$
Answered by ajfour last updated on 04/May/17

Commented by ajfour last updated on 04/May/17
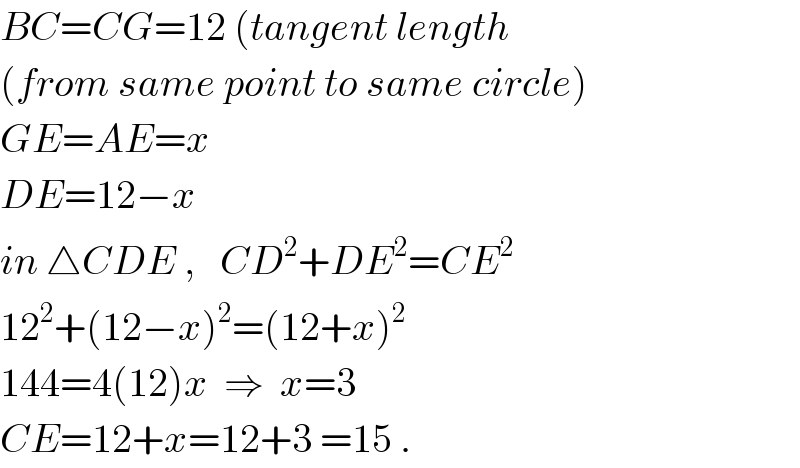
$${BC}={CG}=\mathrm{12}\:\left({tangent}\:{length}\right. \\ $$$$\left({from}\:{same}\:{point}\:{to}\:{same}\:{circle}\right) \\ $$$${GE}={AE}={x} \\ $$$${DE}=\mathrm{12}−{x} \\ $$$${in}\:\bigtriangleup{CDE}\:,\:\:\:{CD}^{\mathrm{2}} +{DE}^{\mathrm{2}} ={CE}^{\mathrm{2}} \\ $$$$\mathrm{12}^{\mathrm{2}} +\left(\mathrm{12}−{x}\right)^{\mathrm{2}} =\left(\mathrm{12}+{x}\right)^{\mathrm{2}} \\ $$$$\mathrm{144}=\mathrm{4}\left(\mathrm{12}\right){x}\:\:\Rightarrow\:\:{x}=\mathrm{3} \\ $$$${CE}=\mathrm{12}+{x}=\mathrm{12}+\mathrm{3}\:=\mathrm{15}\:. \\ $$
Commented by chux last updated on 04/May/17
$$\mathrm{i}\:\mathrm{love}\:\mathrm{this}….\:\mathrm{thanks}\:\mathrm{boss} \\ $$
Commented by A Haq Soomro last updated on 06/May/17

$${Excellent}! \\ $$
