Menu Close

Question-12894

Tinku Tara 0 Comments
Pin




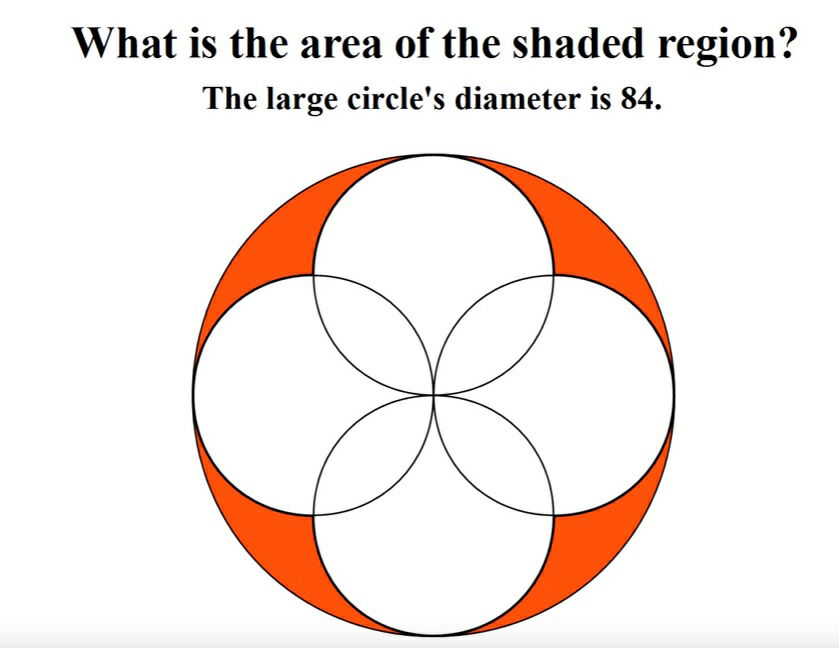
Question Number 12894 by tawa last updated on 06/May/17
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 06/May/17
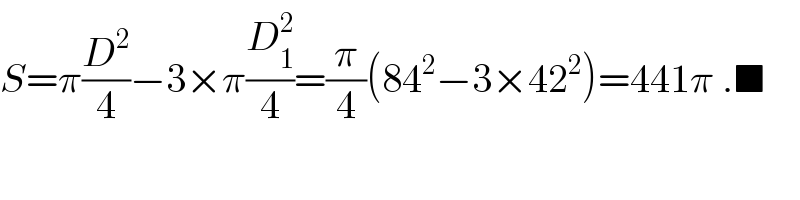
S=π(D^2 /4)−3×π(D_1 ^2 /4)=(π/4)(84^2 −3×42^2 )=441π .■
$${S}=\pi\frac{{D}^{\mathrm{2}} }{\mathrm{4}}−\mathrm{3}×\pi\frac{{D}_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{4}}=\frac{\pi}{\mathrm{4}}\left(\mathrm{84}^{\mathrm{2}} −\mathrm{3}×\mathrm{42}^{\mathrm{2}} \right)=\mathrm{441}\pi\:.\blacksquare \\ $$
Commented by tawa last updated on 06/May/17
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by RasheedSoomro last updated on 06/May/17
Let A is the area of the outer circle, a is an area of smaller circle and c is an common area of any two circles. If S is shaded area then S=A−4a+4c A=π(42)^2 =1764π a=π(21)^2 =441π If s is the segment( half of c) associated with smaller circle then s=Quarter of small circle−a right angled triangle_(whose each leg is 21 ) =((441π)/4)−((21×21)/2)=((441π−2×441)/4)=((441(π−2))/4) c=2s=((441(π−2))/2) S=A−4a+4c=1764π−4(441π)+4(((441(π−2))/2)) =1764π−1764π+882(π−2)=882(π−2)
$$\mathrm{Let}\:{A}\:\:\mathrm{is}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{outer}\:\mathrm{circle}, \\ $$$$\:{a}\:\mathrm{is}\:\mathrm{an}\:\mathrm{area}\:\mathrm{of}\:\mathrm{smaller}\:\mathrm{circle}\:\mathrm{and}\:\:{c} \\ $$$$\mathrm{is}\:\mathrm{an}\:\:\mathrm{common}\:\mathrm{area}\:\mathrm{of}\:\mathrm{any}\:\:\mathrm{two}\:\mathrm{circles}. \\ $$$$\mathrm{If}\:{S}\:\mathrm{is}\:\mathrm{shaded}\:\mathrm{area}\:\mathrm{then} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{S}={A}−\mathrm{4}{a}+\mathrm{4}{c} \\ $$$${A}=\pi\left(\mathrm{42}\right)^{\mathrm{2}} =\mathrm{1764}\pi \\ $$$${a}=\pi\left(\mathrm{21}\right)^{\mathrm{2}} =\mathrm{441}\pi \\ $$$$\mathrm{If}\:{s}\:{is}\:\mathrm{the}\:\mathrm{segment}\left(\:\mathrm{half}\:\mathrm{of}\:{c}\right)\:\:\mathrm{associated} \\ $$$$\mathrm{with}\:\mathrm{smaller}\:\mathrm{circle}\:\mathrm{then} \\ $$$${s}=\mathrm{Quarter}\:\mathrm{of}\:\mathrm{small}\:\mathrm{circle}−\underset{\mathrm{whose}\:\mathrm{each}\:\:\mathrm{leg}\:\:\mathrm{is}\:\:\mathrm{21}\:} {\mathrm{a}\:\mathrm{right}\:\mathrm{angled}\:\mathrm{triangle}} \\ $$$$\:\:\:=\frac{\mathrm{441}\pi}{\mathrm{4}}−\frac{\mathrm{21}×\mathrm{21}}{\mathrm{2}}=\frac{\mathrm{441}\pi−\mathrm{2}×\mathrm{441}}{\mathrm{4}}=\frac{\mathrm{441}\left(\pi−\mathrm{2}\right)}{\mathrm{4}} \\ $$$$ \\ $$$${c}=\mathrm{2}{s}=\frac{\mathrm{441}\left(\pi−\mathrm{2}\right)}{\mathrm{2}} \\ $$$${S}={A}−\mathrm{4}{a}+\mathrm{4}{c}=\mathrm{1764}\pi−\mathrm{4}\left(\mathrm{441}\pi\right)+\mathrm{4}\left(\frac{\mathrm{441}\left(\pi−\mathrm{2}\right)}{\mathrm{2}}\right) \\ $$$$\:\:\:\:=\mathrm{1764}\pi−\mathrm{1764}\pi+\mathrm{882}\left(\pi−\mathrm{2}\right)=\mathrm{882}\left(\pi−\mathrm{2}\right) \\ $$
Commented by tawa last updated on 06/May/17
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by RasheedSoomro last updated on 07/May/17
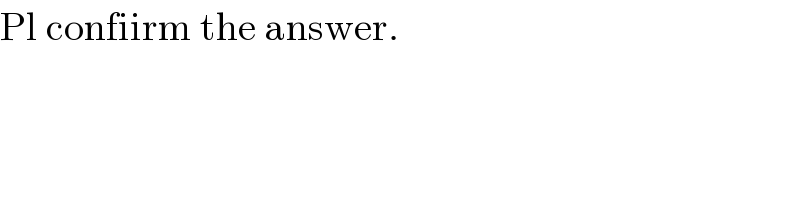
Pl confiirm the answer.
$$\mathrm{Pl}\:\mathrm{confiirm}\:\mathrm{the}\:\mathrm{answer}. \\ $$
Commented by sandy_suhendra last updated on 09/May/17
Commented by sandy_suhendra last updated on 09/May/17
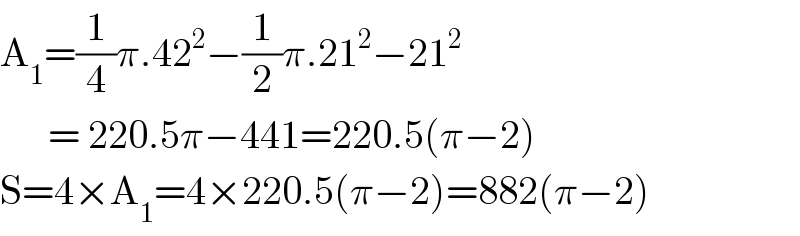
A_1 =(1/4)π.42^2 −(1/2)π.21^2 −21^2 = 220.5π−441=220.5(π−2) S=4×A_1 =4×220.5(π−2)=882(π−2)
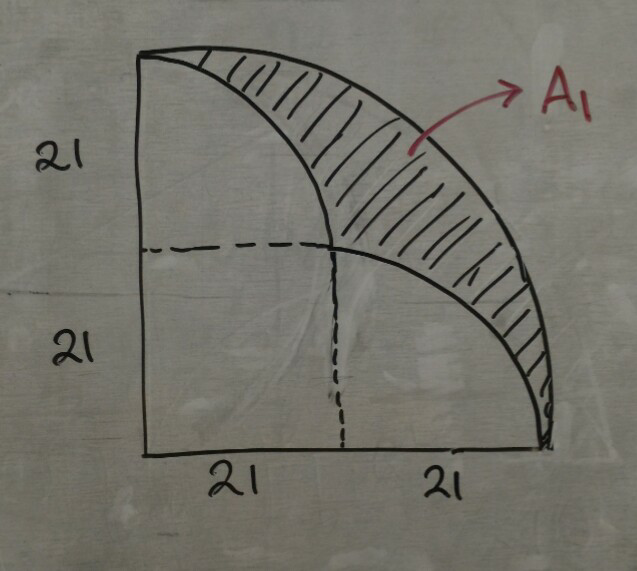
$$\mathrm{A}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{4}}\pi.\mathrm{42}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\pi.\mathrm{21}^{\mathrm{2}} −\mathrm{21}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:=\:\mathrm{220}.\mathrm{5}\pi−\mathrm{441}=\mathrm{220}.\mathrm{5}\left(\pi−\mathrm{2}\right) \\ $$$$\mathrm{S}=\mathrm{4}×\mathrm{A}_{\mathrm{1}} =\mathrm{4}×\mathrm{220}.\mathrm{5}\left(\pi−\mathrm{2}\right)=\mathrm{882}\left(\pi−\mathrm{2}\right)\:\:\:\:\: \\ $$
Commented by RasheedSindhi last updated on 11/May/17
Thanks sandy(my old friend!) Your method is simpler!
$$\mathrm{Thanks}\:\:\mathrm{sandy}\left(\mathrm{my}\:\mathrm{old}\:\mathrm{friend}!\right) \\ $$$$\mathrm{Your}\:\mathrm{method}\:\mathrm{is}\:\mathrm{simpler}! \\ $$
Commented by sandy_suhendra last updated on 18/May/17
hallo Rasheed, why have you changed your user name? And also long time no see you
$$\mathrm{hallo}\:\mathrm{Rasheed},\:\mathrm{why}\:\mathrm{have}\:\mathrm{you}\:\mathrm{changed}\:\mathrm{your}\:\mathrm{user}\:\mathrm{name}? \\ $$$$\mathrm{And}\:\mathrm{also}\:\mathrm{long}\:\mathrm{time}\:\mathrm{no}\:\mathrm{see}\:\mathrm{you} \\ $$
Commented by RasheedSindhi last updated on 19/May/17
ThanX! Actually there′s a weak point of this fine forum that one cannot use unique ID on different devices! Even on same device, after reinstallation changing ID is must! So I use two devices use two ID′s.
$$\mathrm{ThanX}!\:\mathrm{Actually}\:\mathrm{there}'\mathrm{s}\:\:\mathrm{a} \\ $$$$\boldsymbol{\mathrm{weak}}\:\boldsymbol{\mathrm{point}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{this}}\:\boldsymbol{\mathrm{fine}}\:\boldsymbol{\mathrm{forum}} \\ $$$$\boldsymbol{\mathrm{that}}\:\boldsymbol{\mathrm{one}}\:\boldsymbol{\mathrm{cannot}}\:\boldsymbol{\mathrm{use}}\:\boldsymbol{\mathrm{unique}} \\ $$$$\boldsymbol{\mathrm{ID}}\:\boldsymbol{\mathrm{on}}\:\boldsymbol{\mathrm{different}}\:\boldsymbol{\mathrm{devices}}! \\ $$$$\boldsymbol{\mathrm{Even}}\:\boldsymbol{\mathrm{on}}\:\boldsymbol{\mathrm{same}}\:\boldsymbol{\mathrm{device}},\:\boldsymbol{\mathrm{after}}\: \\ $$$$\boldsymbol{\mathrm{reinstallation}}\:\boldsymbol{\mathrm{changing}}\:\boldsymbol{\mathrm{ID}} \\ $$$$\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{must}}! \\ $$$$\mathrm{So}\:\mathrm{I}\:\mathrm{use}\:\mathrm{two}\:\mathrm{devices}\:\mathrm{use}\:\mathrm{two} \\ $$$$\mathrm{ID}'\mathrm{s}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *