Question Number 12930 by tawa last updated on 07/May/17
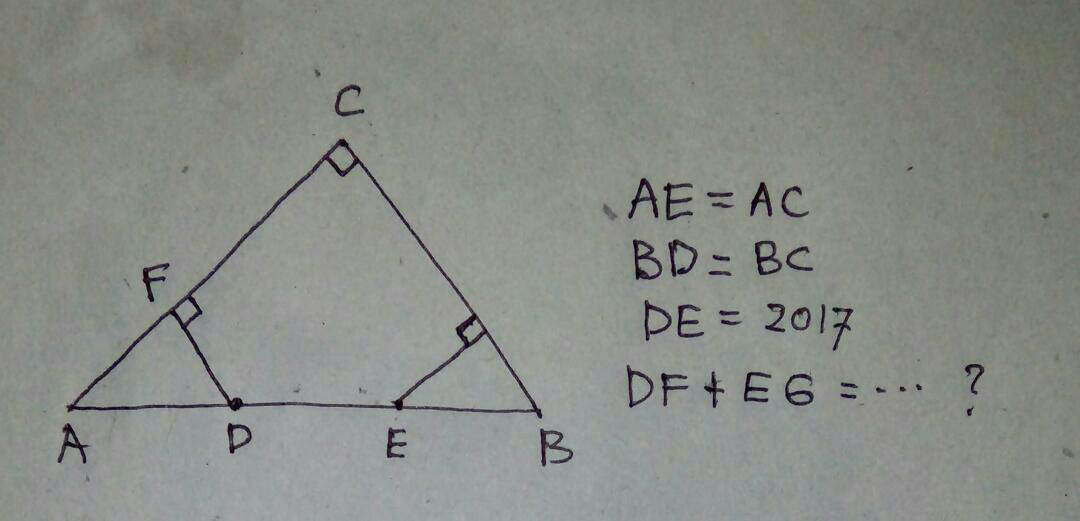
Answered by ajfour last updated on 07/May/17
Commented by ajfour last updated on 07/May/17
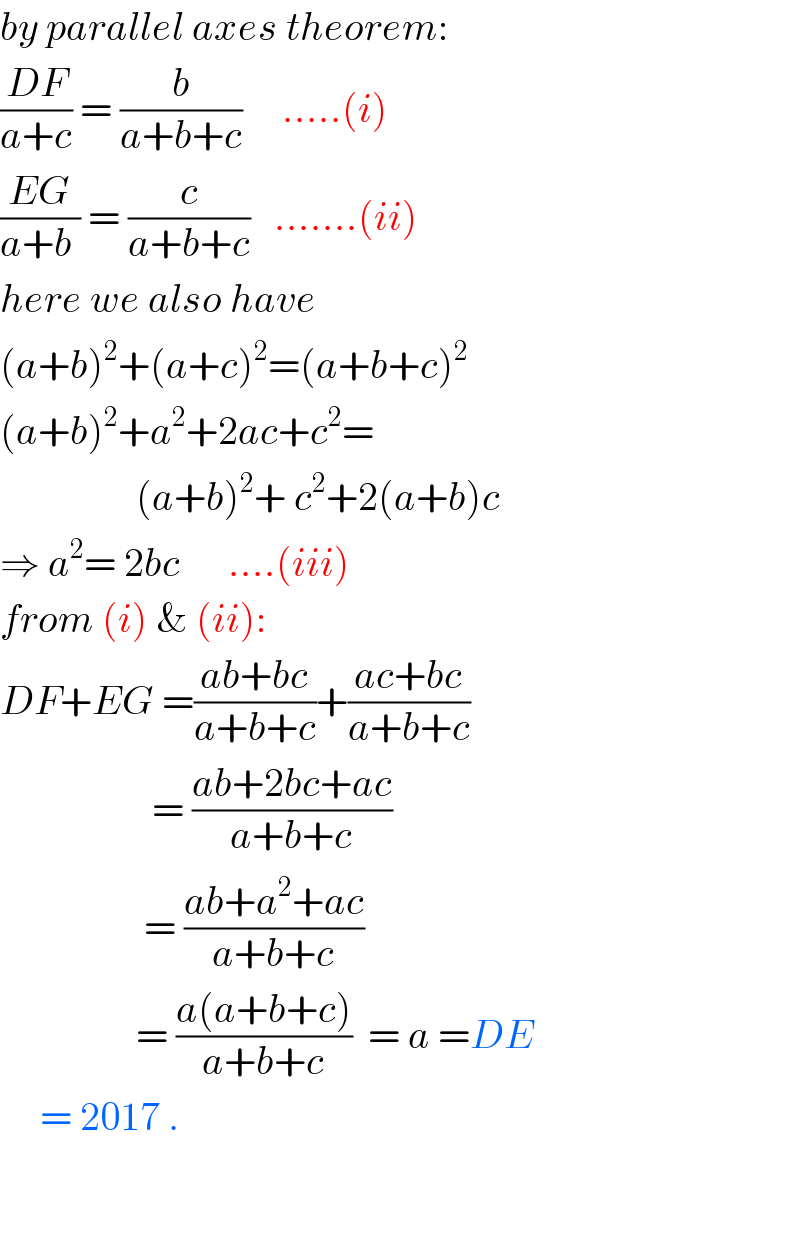
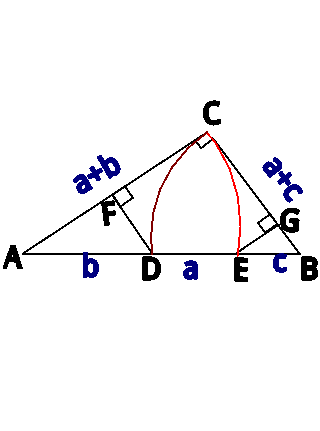
$${by}\:{parallel}\:{axes}\:{theorem}: \\ $$$$\frac{{DF}}{{a}+{c}}\:=\:\frac{{b}}{{a}+{b}+{c}}\:\:\:\:\:…..\left({i}\right) \\ $$$$\frac{{EG}}{{a}+{b}\:}\:=\:\frac{{c}}{{a}+{b}+{c}}\:\:\:…….\left({ii}\right) \\ $$$${here}\:{we}\:{also}\:{have} \\ $$$$\left({a}+{b}\right)^{\mathrm{2}} +\left({a}+{c}\right)^{\mathrm{2}} =\left({a}+{b}+{c}\right)^{\mathrm{2}} \\ $$$$\left({a}+{b}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} +\mathrm{2}{ac}+{c}^{\mathrm{2}} = \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({a}+{b}\right)^{\mathrm{2}} +\:{c}^{\mathrm{2}} +\mathrm{2}\left({a}+{b}\right){c} \\ $$$$\Rightarrow\:{a}^{\mathrm{2}} =\:\mathrm{2}{bc}\:\:\:\:\:\:….\left({iii}\right) \\ $$$${from}\:\left({i}\right)\:\&\:\left({ii}\right): \\ $$$${DF}+{EG}\:=\frac{{ab}+{bc}}{{a}+{b}+{c}}+\frac{{ac}+{bc}}{{a}+{b}+{c}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{{ab}+\mathrm{2}{bc}+{ac}}{{a}+{b}+{c}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{{ab}+{a}^{\mathrm{2}} +{ac}}{{a}+{b}+{c}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{{a}\left({a}+{b}+{c}\right)}{{a}+{b}+{c}}\:\:=\:{a}\:={DE} \\ $$$$\:\:\:\:\:=\:\mathrm{2017}\:. \\ $$$$ \\ $$$$ \\ $$
Commented by tawa last updated on 07/May/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by tawa last updated on 07/May/17

$$\mathrm{Please}\:\mathrm{sir}\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{name}\:\mathrm{of}\:\mathrm{the}\:\mathrm{application}\:\mathrm{you}\:\mathrm{used}\:\mathrm{to}\:\mathrm{draw}\:\mathrm{the}\:\mathrm{diagram} \\ $$
