Question-131121 – Tinku Tara

Question Number 131121 by abdurehime last updated on 01/Feb/21

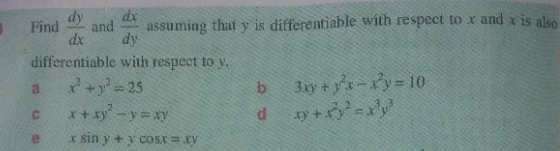
Answered by mathmax by abdo last updated on 01/Feb/21

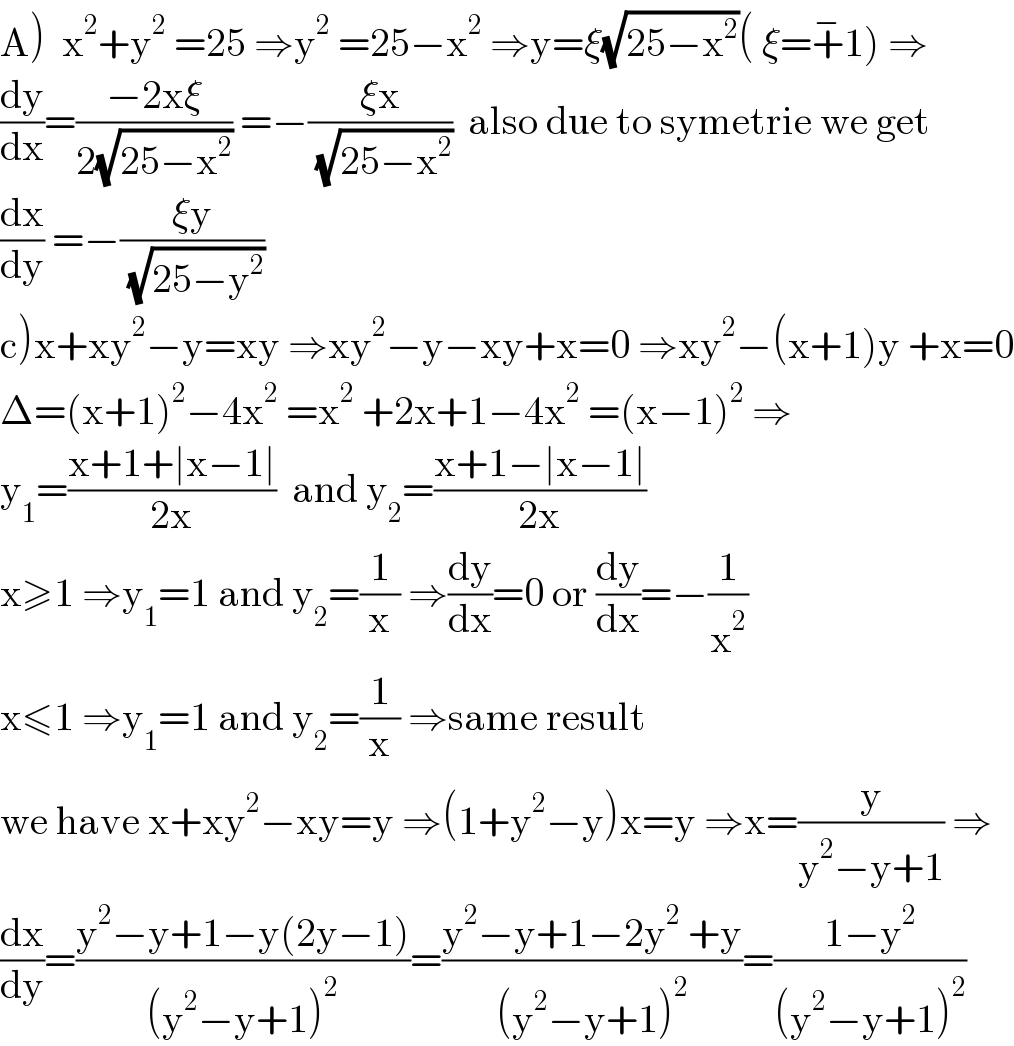
A) x^2 +y^2 =25 ⇒y^2 =25−x^2 ⇒y=ξ(√(25−x^2 ))( ξ=+^− 1) ⇒ (dy/dx)=((−2xξ)/(2(√(25−x^2 )))) =−((ξx)/( (√(25−x^2 )))) also due to symetrie we get (dx/dy) =−((ξy)/( (√(25−y^2 )))) c)x+xy^2 −y=xy ⇒xy^2 −y−xy+x=0 ⇒xy^2 −(x+1)y +x=0 Δ=(x+1)^2 −4x^2 =x^2 +2x+1−4x^2 =(x−1)^2 ⇒ y_1 =((x+1+∣x−1∣)/(2x)) and y_2 =((x+1−∣x−1∣)/(2x)) x≥1 ⇒y_1 =1 and y_2 =(1/x) ⇒(dy/dx)=0 or (dy/dx)=−(1/x^2 ) x≤1 ⇒y_1 =1 and y_2 =(1/x) ⇒same result we have x+xy^2 −xy=y ⇒(1+y^2 −y)x=y ⇒x=(y/(y^2 −y+1)) ⇒ (dx/dy)=((y^2 −y+1−y(2y−1))/((y^2 −y+1)^2 ))=((y^2 −y+1−2y^2 +y)/((y^2 −y+1)^2 ))=((1−y^2 )/((y^2 −y+1)^2 ))

$$\left.\mathrm{A}\right)\:\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \:=\mathrm{25}\:\Rightarrow\mathrm{y}^{\mathrm{2}} \:=\mathrm{25}−\mathrm{x}^{\mathrm{2}} \:\Rightarrow\mathrm{y}=\xi\sqrt{\mathrm{25}−\mathrm{x}^{\mathrm{2}} }\left(\:\xi=\overset{−} {+}\mathrm{1}\right)\:\Rightarrow \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{−\mathrm{2x}\xi}{\mathrm{2}\sqrt{\mathrm{25}−\mathrm{x}^{\mathrm{2}} }}\:=−\frac{\xi\mathrm{x}}{\:\sqrt{\mathrm{25}−\mathrm{x}^{\mathrm{2}} }}\:\:\mathrm{also}\:\mathrm{due}\:\mathrm{to}\:\mathrm{symetrie}\:\mathrm{we}\:\mathrm{get} \\ $$$$\frac{\mathrm{dx}}{\mathrm{dy}}\:=−\frac{\xi\mathrm{y}}{\:\sqrt{\mathrm{25}−\mathrm{y}^{\mathrm{2}} }} \\ $$$$\left.\mathrm{c}\right)\mathrm{x}+\mathrm{xy}^{\mathrm{2}} −\mathrm{y}=\mathrm{xy}\:\Rightarrow\mathrm{xy}^{\mathrm{2}} −\mathrm{y}−\mathrm{xy}+\mathrm{x}=\mathrm{0}\:\Rightarrow\mathrm{xy}^{\mathrm{2}} −\left(\mathrm{x}+\mathrm{1}\right)\mathrm{y}\:+\mathrm{x}=\mathrm{0} \\ $$$$\Delta=\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4x}^{\mathrm{2}} \:=\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{1}−\mathrm{4x}^{\mathrm{2}} \:=\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{y}_{\mathrm{1}} =\frac{\mathrm{x}+\mathrm{1}+\mid\mathrm{x}−\mathrm{1}\mid}{\mathrm{2x}}\:\:\mathrm{and}\:\mathrm{y}_{\mathrm{2}} =\frac{\mathrm{x}+\mathrm{1}−\mid\mathrm{x}−\mathrm{1}\mid}{\mathrm{2x}} \\ $$$$\mathrm{x}\geqslant\mathrm{1}\:\Rightarrow\mathrm{y}_{\mathrm{1}} =\mathrm{1}\:\mathrm{and}\:\mathrm{y}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{x}}\:\Rightarrow\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{0}\:\mathrm{or}\:\frac{\mathrm{dy}}{\mathrm{dx}}=−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{x}\leqslant\mathrm{1}\:\Rightarrow\mathrm{y}_{\mathrm{1}} =\mathrm{1}\:\mathrm{and}\:\mathrm{y}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{x}}\:\Rightarrow\mathrm{same}\:\mathrm{result} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{x}+\mathrm{xy}^{\mathrm{2}} −\mathrm{xy}=\mathrm{y}\:\Rightarrow\left(\mathrm{1}+\mathrm{y}^{\mathrm{2}} −\mathrm{y}\right)\mathrm{x}=\mathrm{y}\:\Rightarrow\mathrm{x}=\frac{\mathrm{y}}{\mathrm{y}^{\mathrm{2}} −\mathrm{y}+\mathrm{1}}\:\Rightarrow \\ $$$$\frac{\mathrm{dx}}{\mathrm{dy}}=\frac{\mathrm{y}^{\mathrm{2}} −\mathrm{y}+\mathrm{1}−\mathrm{y}\left(\mathrm{2y}−\mathrm{1}\right)}{\left(\mathrm{y}^{\mathrm{2}} −\mathrm{y}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{y}^{\mathrm{2}} −\mathrm{y}+\mathrm{1}−\mathrm{2y}^{\mathrm{2}} \:+\mathrm{y}}{\left(\mathrm{y}^{\mathrm{2}} −\mathrm{y}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{1}−\mathrm{y}^{\mathrm{2}} }{\left(\mathrm{y}^{\mathrm{2}} −\mathrm{y}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$

Commented by abdurehime last updated on 02/Feb/21

$$\mathrm{thank}\:\mathrm{u} \\ $$

Answered by liberty last updated on 02/Feb/21

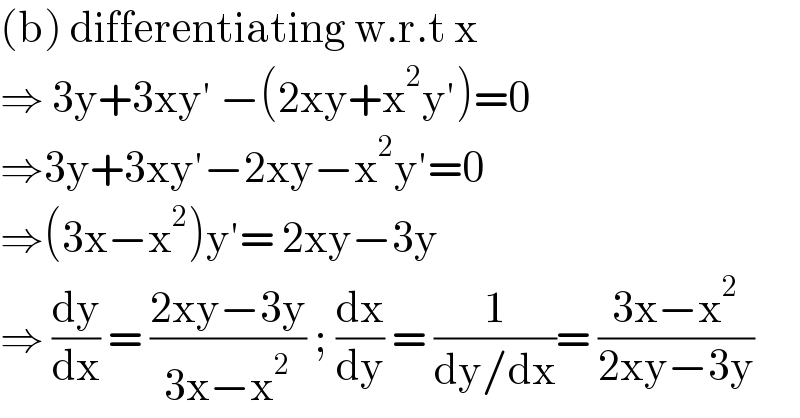
(b) differentiating w.r.t x ⇒ 3y+3xy′ −(2xy+x^2 y′)=0 ⇒3y+3xy′−2xy−x^2 y′=0 ⇒(3x−x^2 )y′= 2xy−3y ⇒ (dy/dx) = ((2xy−3y)/(3x−x^2 )) ; (dx/dy) = (1/(dy/dx))= ((3x−x^2 )/(2xy−3y))

$$\left(\mathrm{b}\right)\:\mathrm{differentiating}\:\mathrm{w}.\mathrm{r}.\mathrm{t}\:\mathrm{x} \\ $$$$\Rightarrow\:\mathrm{3y}+\mathrm{3xy}'\:−\left(\mathrm{2xy}+\mathrm{x}^{\mathrm{2}} \mathrm{y}'\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{3y}+\mathrm{3xy}'−\mathrm{2xy}−\mathrm{x}^{\mathrm{2}} \mathrm{y}'=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{3x}−\mathrm{x}^{\mathrm{2}} \right)\mathrm{y}'=\:\mathrm{2xy}−\mathrm{3y}\: \\ $$$$\Rightarrow\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{2xy}−\mathrm{3y}}{\mathrm{3x}−\mathrm{x}^{\mathrm{2}} }\:;\:\frac{\mathrm{dx}}{\mathrm{dy}}\:=\:\frac{\mathrm{1}}{\mathrm{dy}/\mathrm{dx}}=\:\frac{\mathrm{3x}−\mathrm{x}^{\mathrm{2}} }{\mathrm{2xy}−\mathrm{3y}} \\ $$

Answered by liberty last updated on 02/Feb/21

(a) (d/dx)[x^2 +y^2 ] = 0 ⇒ 2x+2y(dy/dx) = 0 ; (dy/dx)=−(x/y) ∧ (dx/dy)=−(y/x) where y = ±(√(25−x^2 ))

$$\left(\mathrm{a}\right)\:\frac{\mathrm{d}}{\mathrm{dx}}\left[\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \:\right]\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{2x}+\mathrm{2y}\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{0}\:;\:\frac{\mathrm{dy}}{\mathrm{dx}}=−\frac{\mathrm{x}}{\mathrm{y}}\:\wedge\:\frac{\mathrm{dx}}{\mathrm{dy}}=−\frac{\mathrm{y}}{\mathrm{x}} \\ $$$$\mathrm{where}\:\mathrm{y}\:=\:\pm\sqrt{\mathrm{25}−\mathrm{x}^{\mathrm{2}} } \\ $$$$ \\ $$

Facebook Tweet Pin