Menu Close

Question-131167

Tinku Tara
Pin




Question Number 131167 by 676597498 last updated on 02/Feb/21
Answered by SEKRET last updated on 02/Feb/21
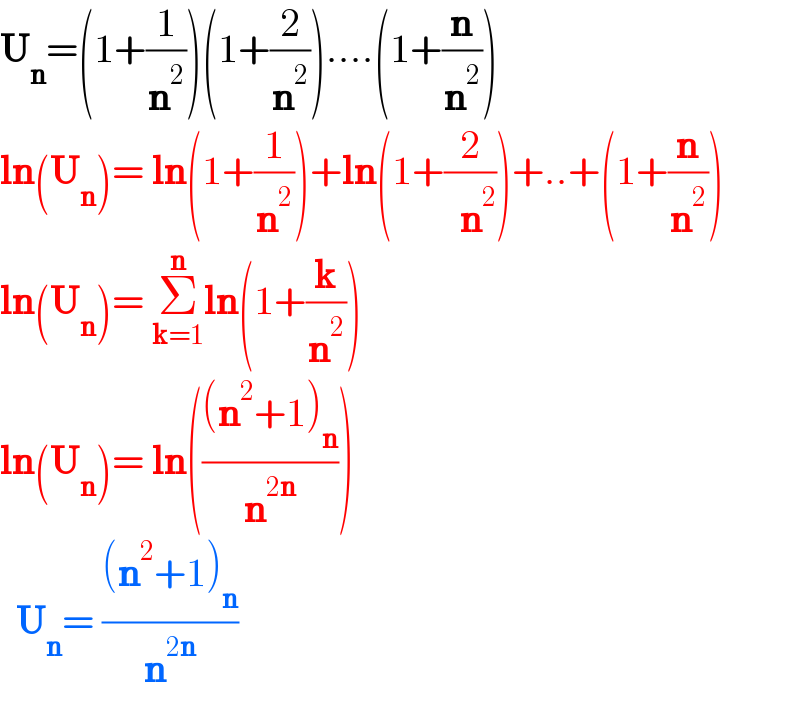
U_n =(1+(1/n^2 ))(1+(2/n^2 ))....(1+(n/n^2 )) ln(U_n )= ln(1+(1/n^2 ))+ln(1+(2/( n^2 )))+..+(1+(n/n^2 )) ln(U_n )= Σ_(k=1) ^n ln(1+(k/n^2 )) ln(U_n )= ln((((n^2 +1)_n )/n^(2n) )) U_n = (((n^2 +1)_n )/n^(2n) )
$$\boldsymbol{\mathrm{U}}_{\boldsymbol{\mathrm{n}}} =\left(\mathrm{1}+\frac{\mathrm{1}}{\boldsymbol{\mathrm{n}}^{\mathrm{2}} }\right)\left(\mathrm{1}+\frac{\mathrm{2}}{\boldsymbol{\mathrm{n}}^{\mathrm{2}} }\right)….\left(\mathrm{1}+\frac{\boldsymbol{\mathrm{n}}}{\boldsymbol{\mathrm{n}}^{\mathrm{2}} }\right) \\ $$$$\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{U}}_{\boldsymbol{\mathrm{n}}} \right)=\:\boldsymbol{\mathrm{ln}}\left(\mathrm{1}+\frac{\mathrm{1}}{\boldsymbol{\mathrm{n}}^{\mathrm{2}} }\right)+\boldsymbol{\mathrm{ln}}\left(\mathrm{1}+\frac{\mathrm{2}}{\:\:\boldsymbol{\mathrm{n}}^{\mathrm{2}} }\right)+..+\left(\mathrm{1}+\frac{\boldsymbol{\mathrm{n}}}{\boldsymbol{\mathrm{n}}^{\mathrm{2}} }\right) \\ $$$$\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{U}}_{\boldsymbol{\mathrm{n}}} \right)=\:\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\boldsymbol{\mathrm{n}}} {\sum}}\boldsymbol{\mathrm{ln}}\left(\mathrm{1}+\frac{\boldsymbol{\mathrm{k}}}{\boldsymbol{\mathrm{n}}^{\mathrm{2}} }\right) \\ $$$$\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{U}}_{\boldsymbol{\mathrm{n}}} \right)=\:\boldsymbol{\mathrm{ln}}\left(\frac{\left(\boldsymbol{\mathrm{n}}^{\mathrm{2}} +\mathrm{1}\right)_{\boldsymbol{\mathrm{n}}} }{\boldsymbol{\mathrm{n}}^{\mathrm{2}\boldsymbol{\mathrm{n}}} }\right) \\ $$$$\:\:\boldsymbol{\mathrm{U}}_{\boldsymbol{\mathrm{n}}} =\:\frac{\left(\boldsymbol{\mathrm{n}}^{\mathrm{2}} +\mathrm{1}\right)_{\boldsymbol{\mathrm{n}}} }{\boldsymbol{\mathrm{n}}^{\mathrm{2}\boldsymbol{\mathrm{n}}} } \\ $$
Commented by 676597498 last updated on 02/Feb/21
i dont get it
$$\mathrm{i}\:\mathrm{dont}\:\mathrm{get}\:\mathrm{it} \\ $$
Answered by mathmax by abdo last updated on 02/Feb/21
u_n =Π_(k=1) ^n (1+(k/n^2 )) ⇒v_n =ln(u_n )=Σ_(k=1) ^n ln(1+(k/n^2 )) let prove first x−(x^2 /2)≤ln(1+x)≤x let f(x)=x−ln(1+x) withx≥0 f^′ (x)=1−(1/(1+x))=(x/(1+x))≥0 ⇒f is increazinz but f(0)=0 ⇒f(x)≥0 ⇒ x≥ln(1+x) let g(x)=ln(1+x)−x+(x^2 /2) ⇒ g^′ (x)=(1/(1+x))−1+x =((1+x^2 −1)/(1+x))=(x^2 /(1+x))≥0 ⇒g is increazing but g(o)=0 ⇒g(x)≥0 ⇒x−(x^2 /2)≤ln(1+x)≤x ⇒ (k/n^2 )−(k^2 /(2n^4 ))≤ln(1+(k/n^2 ))≤(k/n^2 ) ⇒ (1/n^2 )Σ_(k=1) ^n k−(1/(2n^4 ))Σ_(k=1) ^n k^2 ≤v_n ≤(1/n^2 )Σ_(k=1) ^n k ⇒ (1/n^2 )×((n(n+1))/2)−(1/(2n^4 ))((n(n+1)(2n+1))/6)≤v_n ≤(1/n^2 )×((n(n+1))/2) ⇒ ((n^2 +n)/(2n^2 ))−(((n+1)(2n+1))/(12n^3 ))≤v_n ≤((n^2 +n)/(2n^2 )) ⇒ ((n+1)/(2n))−(((n+1)(2n+1))/(12n^3 ))≤v_n ≤((n+1)/(2n)) ⇒lim_(n→+∞) =(1/2) ⇒ lim_(n→+∞) ln(u_n )=(1/2) ⇒lim_(n→+∞) u_n =e^(1/2) =(√e)
$$\mathrm{u}_{\mathrm{n}} =\prod_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}^{\mathrm{2}} }\right)\:\Rightarrow\mathrm{v}_{\mathrm{n}} =\mathrm{ln}\left(\mathrm{u}_{\mathrm{n}} \right)=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}^{\mathrm{2}} }\right) \\ $$$$\mathrm{let}\:\mathrm{prove}\:\mathrm{first}\:\mathrm{x}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\leqslant\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\leqslant\mathrm{x}\:\:\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}−\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\:\mathrm{withx}\geqslant\mathrm{0} \\ $$$$\mathrm{f}^{'} \left(\mathrm{x}\right)=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}=\frac{\mathrm{x}}{\mathrm{1}+\mathrm{x}}\geqslant\mathrm{0}\:\Rightarrow\mathrm{f}\:\mathrm{is}\:\mathrm{increazinz}\:\mathrm{but}\:\mathrm{f}\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\geqslant\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{x}\geqslant\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\:\mathrm{let}\:\mathrm{g}\left(\mathrm{x}\right)=\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)−\mathrm{x}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{g}^{'} \left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}−\mathrm{1}+\mathrm{x}\:=\frac{\mathrm{1}+\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}+\mathrm{x}}=\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{x}}\geqslant\mathrm{0}\:\:\Rightarrow\mathrm{g}\:\mathrm{is}\:\mathrm{increazing}\:\:\mathrm{but} \\ $$$$\mathrm{g}\left(\mathrm{o}\right)=\mathrm{0}\:\Rightarrow\mathrm{g}\left(\mathrm{x}\right)\geqslant\mathrm{0}\:\Rightarrow\mathrm{x}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\leqslant\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\leqslant\mathrm{x}\:\Rightarrow \\ $$$$\frac{\mathrm{k}}{\mathrm{n}^{\mathrm{2}} }−\frac{\mathrm{k}^{\mathrm{2}} }{\mathrm{2n}^{\mathrm{4}} }\leqslant\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}^{\mathrm{2}} }\right)\leqslant\frac{\mathrm{k}}{\mathrm{n}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{k}−\frac{\mathrm{1}}{\mathrm{2n}^{\mathrm{4}} }\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{k}^{\mathrm{2}} \:\leqslant\mathrm{v}_{\mathrm{n}} \leqslant\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{k}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }×\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2n}^{\mathrm{4}} }\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2n}+\mathrm{1}\right)}{\mathrm{6}}\leqslant\mathrm{v}_{\mathrm{n}} \leqslant\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }×\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}}\:\Rightarrow \\ $$$$\frac{\mathrm{n}^{\mathrm{2}} \:+\mathrm{n}}{\mathrm{2n}^{\mathrm{2}} }−\frac{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2n}+\mathrm{1}\right)}{\mathrm{12n}^{\mathrm{3}} }\leqslant\mathrm{v}_{\mathrm{n}} \leqslant\frac{\mathrm{n}^{\mathrm{2}} \:+\mathrm{n}}{\mathrm{2n}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2n}}−\frac{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{2n}+\mathrm{1}\right)}{\mathrm{12n}^{\mathrm{3}} }\leqslant\mathrm{v}_{\mathrm{n}} \leqslant\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2n}}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} =\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{ln}\left(\mathrm{u}_{\mathrm{n}} \right)=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{u}_{\mathrm{n}} =\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}}} \:=\sqrt{\mathrm{e}} \\ $$

Pin