Menu Close

Question-131201

Tinku Tara
Pin




Question Number 131201 by shaker last updated on 02/Feb/21
Answered by liberty last updated on 11/Feb/21
L=∫ ((tan^2 x)/(cos 2x)) dx ; by change of variable let u = tan x → { ((dx=(du/(1+u^2 )))),((cos 2x=((1−u^2 )/(1+u^2 )))) :} L=∫ (((u^2 (1+u^2 ))/(1−u^2 )))((du/(1+u^2 ))) L=∫ (u^2 /(1−u^2 )) du = ∫ (−1−(1/(1−u^2 )))du L=−u−(1/2)∫ [ (1/(1−u))+(1/(1+u)) ]du L=−u−(1/2)ln ∣((1+u)/(1−u)) ∣+c L=−tan x−(1/2)ln ∣((tan x+1)/(1−tan x)) ∣ + c
$$\mathrm{L}=\int\:\frac{\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{cos}\:\mathrm{2x}}\:\mathrm{dx}\:;\:\mathrm{by}\:\mathrm{change}\:\mathrm{of}\:\mathrm{variable}\: \\ $$$$\:\mathrm{let}\:\mathrm{u}\:=\:\mathrm{tan}\:\mathrm{x}\:\rightarrow\begin{cases}{\mathrm{dx}=\frac{\mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }}\\{\mathrm{cos}\:\mathrm{2x}=\frac{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }}\end{cases} \\ $$$$\mathrm{L}=\int\:\left(\frac{\mathrm{u}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)}{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }\right)\left(\frac{\mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\right) \\ $$$$\mathrm{L}=\int\:\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }\:\mathrm{du}\:=\:\int\:\left(−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }\right)\mathrm{du} \\ $$$$\mathrm{L}=−\mathrm{u}−\frac{\mathrm{1}}{\mathrm{2}}\int\:\left[\:\frac{\mathrm{1}}{\mathrm{1}−\mathrm{u}}+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{u}}\:\right]\mathrm{du} \\ $$$$\mathrm{L}=−\mathrm{u}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\frac{\mathrm{1}+\mathrm{u}}{\mathrm{1}−\mathrm{u}}\:\mid+\mathrm{c} \\ $$$$\mathrm{L}=−\mathrm{tan}\:\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\frac{\mathrm{tan}\:\mathrm{x}+\mathrm{1}}{\mathrm{1}−\mathrm{tan}\:\mathrm{x}}\:\mid\:+\:\mathrm{c} \\ $$
Answered by mathmax by abdo last updated on 02/Feb/21
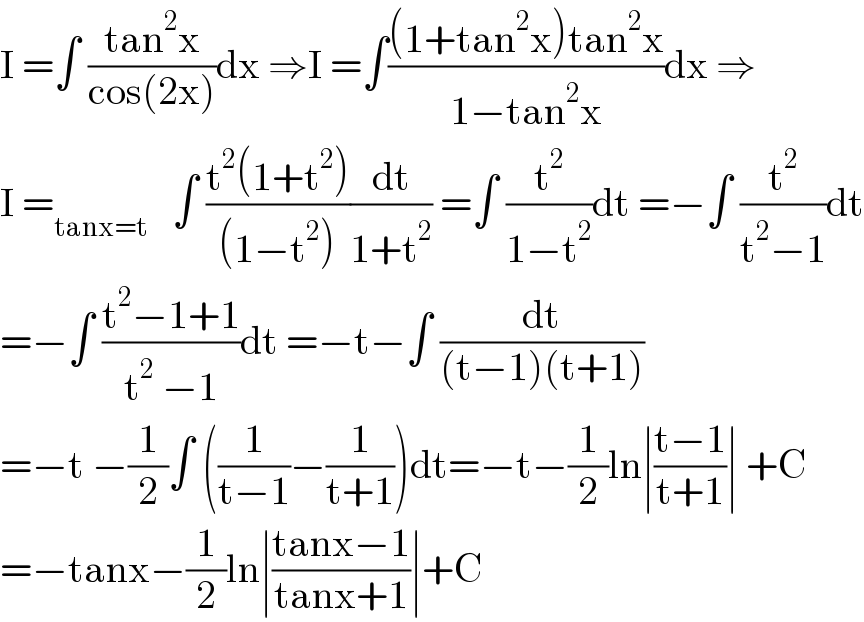
I =∫ ((tan^2 x)/(cos(2x)))dx ⇒I =∫(((1+tan^2 x)tan^2 x)/(1−tan^2 x))dx ⇒ I =_(tanx=t) ∫ ((t^2 (1+t^2 ))/((1−t^2 )))(dt/(1+t^2 )) =∫ (t^2 /(1−t^2 ))dt =−∫ (t^2 /(t^2 −1))dt =−∫ ((t^2 −1+1)/(t^2 −1))dt =−t−∫ (dt/((t−1)(t+1))) =−t −(1/2)∫ ((1/(t−1))−(1/(t+1)))dt=−t−(1/2)ln∣((t−1)/(t+1))∣ +C =−tanx−(1/2)ln∣((tanx−1)/(tanx+1))∣+C
$$\mathrm{I}\:=\int\:\frac{\mathrm{tan}^{\mathrm{2}} \mathrm{x}}{\mathrm{cos}\left(\mathrm{2x}\right)}\mathrm{dx}\:\Rightarrow\mathrm{I}\:=\int\frac{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)\mathrm{tan}^{\mathrm{2}} \mathrm{x}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{I}\:=_{\mathrm{tanx}=\mathrm{t}} \:\:\:\int\:\frac{\mathrm{t}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}{\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)}\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:=\int\:\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:=−\int\:\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\mathrm{dt} \\ $$$$=−\int\:\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}}{\mathrm{t}^{\mathrm{2}} \:−\mathrm{1}}\mathrm{dt}\:=−\mathrm{t}−\int\:\frac{\mathrm{dt}}{\left(\mathrm{t}−\mathrm{1}\right)\left(\mathrm{t}+\mathrm{1}\right)} \\ $$$$=−\mathrm{t}\:−\frac{\mathrm{1}}{\mathrm{2}}\int\:\left(\frac{\mathrm{1}}{\mathrm{t}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{t}+\mathrm{1}}\right)\mathrm{dt}=−\mathrm{t}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{t}−\mathrm{1}}{\mathrm{t}+\mathrm{1}}\mid\:+\mathrm{C} \\ $$$$=−\mathrm{tanx}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{tanx}−\mathrm{1}}{\mathrm{tanx}+\mathrm{1}}\mid+\mathrm{C} \\ $$

Pin