Menu Close

Question-131214

Tinku Tara
Pin




Question Number 131214 by shaker last updated on 02/Feb/21
Answered by Ar Brandon last updated on 02/Feb/21
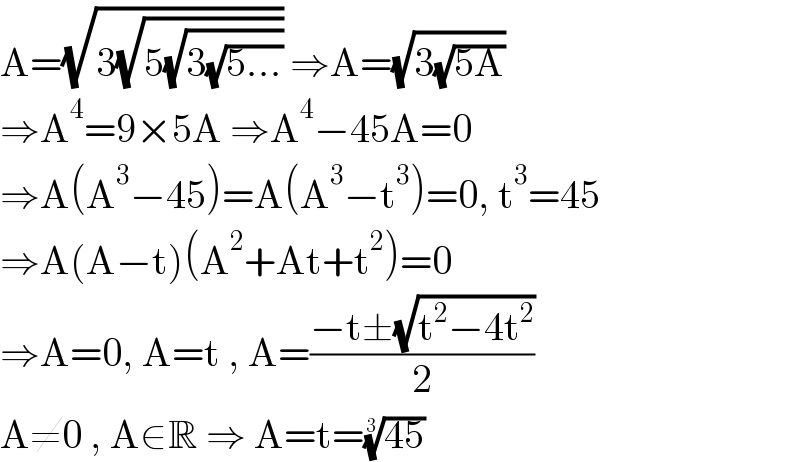
A=(√(3(√(5(√(3(√(5...)))))))) ⇒A=(√(3(√(5A)))) ⇒A^4 =9×5A ⇒A^4 −45A=0 ⇒A(A^3 −45)=A(A^3 −t^3 )=0, t^3 =45 ⇒A(A−t)(A^2 +At+t^2 )=0 ⇒A=0, A=t , A=((−t±(√(t^2 −4t^2 )))/2) A≠0 , A∈R ⇒ A=t=((45))^(1/3)
$$\mathrm{A}=\sqrt{\mathrm{3}\sqrt{\mathrm{5}\sqrt{\mathrm{3}\sqrt{\mathrm{5}…}}}}\:\Rightarrow\mathrm{A}=\sqrt{\mathrm{3}\sqrt{\mathrm{5A}}} \\ $$$$\Rightarrow\mathrm{A}^{\mathrm{4}} =\mathrm{9}×\mathrm{5A}\:\Rightarrow\mathrm{A}^{\mathrm{4}} −\mathrm{45A}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{A}\left(\mathrm{A}^{\mathrm{3}} −\mathrm{45}\right)=\mathrm{A}\left(\mathrm{A}^{\mathrm{3}} −\mathrm{t}^{\mathrm{3}} \right)=\mathrm{0},\:\mathrm{t}^{\mathrm{3}} =\mathrm{45} \\ $$$$\Rightarrow\mathrm{A}\left(\mathrm{A}−\mathrm{t}\right)\left(\mathrm{A}^{\mathrm{2}} +\mathrm{At}+\mathrm{t}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{A}=\mathrm{0},\:\mathrm{A}=\mathrm{t}\:,\:\mathrm{A}=\frac{−\mathrm{t}\pm\sqrt{\mathrm{t}^{\mathrm{2}} −\mathrm{4t}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\mathrm{A}\neq\mathrm{0}\:,\:\mathrm{A}\in\mathbb{R}\:\Rightarrow\:\mathrm{A}=\mathrm{t}=\sqrt[{\mathrm{3}}]{\mathrm{45}} \\ $$
Commented by malwan last updated on 02/Feb/21
thank you so much sir
Commented by Ar Brandon last updated on 02/Feb/21
You're welcome, Sir

Pin