Question Number 131288 by mohammad17 last updated on 03/Feb/21

Answered by liberty last updated on 11/Feb/21

$$\mathrm{L}=\int\:\sqrt{\frac{\mathrm{1}−\mathrm{3x}^{−\mathrm{3}} }{\mathrm{x}^{\mathrm{8}} }}\:\mathrm{dx}\:=\:\int\:\mathrm{x}^{−\mathrm{4}} \:\sqrt{\mathrm{1}−\mathrm{3x}^{−\mathrm{3}} }\:\mathrm{dx} \\ $$$$\mathrm{change}\:\mathrm{of}\:\mathrm{variable}\::\:\sqrt{\mathrm{1}−\mathrm{3x}^{−\mathrm{3}} }\:=\:\mathrm{h}\:\mathrm{or}\:\mathrm{1}−\mathrm{3x}^{−\mathrm{3}} =\mathrm{h}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{9x}^{−\mathrm{4}} \:\mathrm{dx}\:=\:\mathrm{2h}\:\mathrm{dh} \\ $$$$\mathrm{L}\:=\:\frac{\mathrm{2}}{\mathrm{9}}\int\:\mathrm{h}^{\mathrm{2}} \:\mathrm{dh}\:=\:\frac{\mathrm{2}}{\mathrm{27}}\mathrm{h}^{\mathrm{3}} \:+\:\mathrm{c}\: \\ $$$$\mathrm{L}=\frac{\mathrm{2}}{\mathrm{27}}\:\sqrt{\left(\frac{\mathrm{x}^{\mathrm{3}} −\mathrm{3}}{\mathrm{x}^{\mathrm{3}} }\right)^{\mathrm{3}} }\:+\:\mathrm{c}\:=\frac{\mathrm{2}}{\mathrm{27}}\left(\frac{\mathrm{x}^{\mathrm{3}} −\mathrm{3}}{\mathrm{x}^{\mathrm{3}} }\right)\:\sqrt{\frac{\mathrm{x}^{\mathrm{3}} −\mathrm{3}}{\mathrm{x}^{\mathrm{3}} }}\:+\:\mathrm{c} \\ $$
Answered by Dwaipayan Shikari last updated on 03/Feb/21
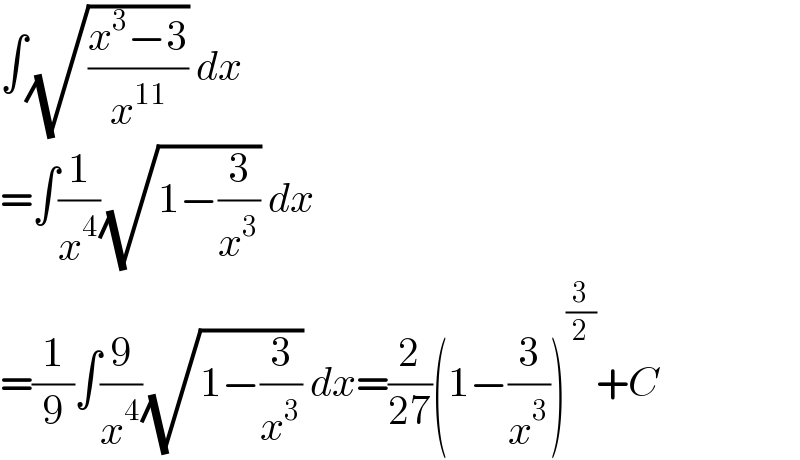
$$\int\sqrt{\frac{{x}^{\mathrm{3}} −\mathrm{3}}{{x}^{\mathrm{11}} }}\:{dx} \\ $$$$=\int\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\sqrt{\mathrm{1}−\frac{\mathrm{3}}{{x}^{\mathrm{3}} }}\:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\int\frac{\mathrm{9}}{{x}^{\mathrm{4}} }\sqrt{\mathrm{1}−\frac{\mathrm{3}}{{x}^{\mathrm{3}} }}\:{dx}=\frac{\mathrm{2}}{\mathrm{27}}\left(\mathrm{1}−\frac{\mathrm{3}}{{x}^{\mathrm{3}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +{C} \\ $$
