Menu Close

Question-131325

Tinku Tara
Pin




Question Number 131325 by mohammad17 last updated on 03/Feb/21
Commented by mohammad17 last updated on 03/Feb/21
find n
$${find}\:{n} \\ $$
Answered by mr W last updated on 04/Feb/21
no solution for n∈Z! for n∈C: (1+i)^n =−(1/8)(1+i) (1+i)^(n−1) =−(1/8) ((√2)e^((πi)/4) )^(n−1) =(1/8)e^((2k+1)πi) (e^(ln (√2)+((πi)/4)) )^(n−1) =e^(−3ln 2+(2k+1)πi) (n−1)((1/2)ln 2+((πi)/4))=−3ln 2+(2k+1)πi ⇒n=1+((4(−3ln 2+(2k+1)πi))/(2 ln 2+πi)) ⇒n=1+((4(−3ln 2+(2k+1)πi)(2 ln 2−πi))/(4(ln 2)^2 +π^2 )) ⇒n=(((8k+5)π^2 −20(ln 2)^2 +4(4k+5)πi)/(4(ln 2)^2 +π^2 ))
$${no}\:{solution}\:{for}\:{n}\in{Z}! \\ $$$$ \\ $$$${for}\:{n}\in{C}: \\ $$$$\left(\mathrm{1}+{i}\right)^{{n}} =−\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{1}+{i}\right) \\ $$$$\left(\mathrm{1}+{i}\right)^{{n}−\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\left(\sqrt{\mathrm{2}}{e}^{\frac{\pi{i}}{\mathrm{4}}} \right)^{{n}−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{8}}{e}^{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi{i}} \\ $$$$\left({e}^{\mathrm{ln}\:\sqrt{\mathrm{2}}+\frac{\pi{i}}{\mathrm{4}}} \right)^{{n}−\mathrm{1}} ={e}^{−\mathrm{3ln}\:\mathrm{2}+\left(\mathrm{2}{k}+\mathrm{1}\right)\pi{i}} \\ $$$$\left({n}−\mathrm{1}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mathrm{2}+\frac{\pi{i}}{\mathrm{4}}\right)=−\mathrm{3ln}\:\mathrm{2}+\left(\mathrm{2}{k}+\mathrm{1}\right)\pi{i} \\ $$$$\Rightarrow{n}=\mathrm{1}+\frac{\mathrm{4}\left(−\mathrm{3ln}\:\mathrm{2}+\left(\mathrm{2}{k}+\mathrm{1}\right)\pi{i}\right)}{\mathrm{2}\:\mathrm{ln}\:\mathrm{2}+\pi{i}} \\ $$$$\Rightarrow{n}=\mathrm{1}+\frac{\mathrm{4}\left(−\mathrm{3ln}\:\mathrm{2}+\left(\mathrm{2}{k}+\mathrm{1}\right)\pi{i}\right)\left(\mathrm{2}\:\mathrm{ln}\:\mathrm{2}−\pi{i}\right)}{\mathrm{4}\left(\mathrm{ln}\:\mathrm{2}\right)^{\mathrm{2}} +\pi^{\mathrm{2}} } \\ $$$$\Rightarrow{n}=\frac{\left(\mathrm{8}{k}+\mathrm{5}\right)\pi^{\mathrm{2}} −\mathrm{20}\left(\mathrm{ln}\:\mathrm{2}\right)^{\mathrm{2}} +\mathrm{4}\left(\mathrm{4}{k}+\mathrm{5}\right)\pi{i}}{\mathrm{4}\left(\mathrm{ln}\:\mathrm{2}\right)^{\mathrm{2}} +\pi^{\mathrm{2}} } \\ $$
Commented by MJS_new last updated on 04/Feb/21
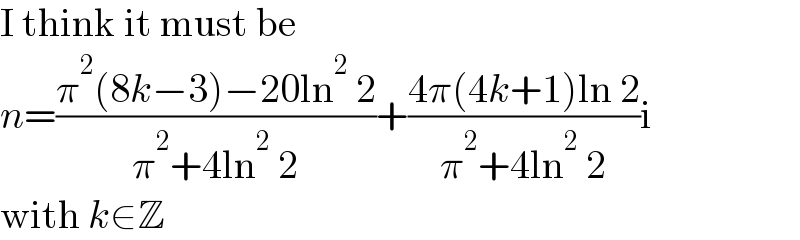
I think it must be n=((π^2 (8k−3)−20ln^2 2)/(π^2 +4ln^2 2))+((4π(4k+1)ln 2)/(π^2 +4ln^2 2))i with k∈Z
$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{must}\:\mathrm{be} \\ $$$${n}=\frac{\pi^{\mathrm{2}} \left(\mathrm{8}{k}−\mathrm{3}\right)−\mathrm{20ln}^{\mathrm{2}} \:\mathrm{2}}{\pi^{\mathrm{2}} +\mathrm{4ln}^{\mathrm{2}} \:\mathrm{2}}+\frac{\mathrm{4}\pi\left(\mathrm{4}{k}+\mathrm{1}\right)\mathrm{ln}\:\mathrm{2}}{\pi^{\mathrm{2}} +\mathrm{4ln}^{\mathrm{2}} \:\mathrm{2}}\mathrm{i} \\ $$$$\mathrm{with}\:{k}\in\mathbb{Z} \\ $$
Commented by mr W last updated on 04/Feb/21
you are right. thanks!
$${you}\:{are}\:{right}. \\ $$$${thanks}! \\ $$

Pin