Menu Close

Question-131328

Tinku Tara
Pin




Question Number 131328 by rs4089 last updated on 03/Feb/21
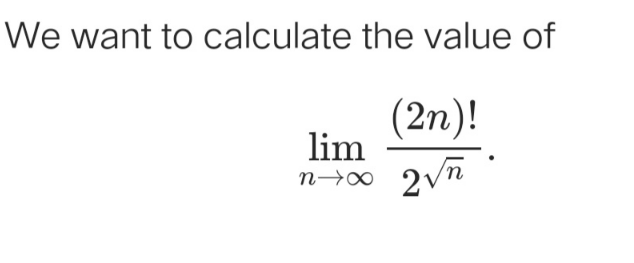
Commented by MJS_new last updated on 04/Feb/21
really? just try some values with n=k^2 ∧k∈N y_k =(((2k^2 )!)/2^k ) y_1 =1 y_2 =10080 y_3 =800296713216000 ... y_(10) ≈7.70×10^(371) ... ⇒ the answer is +∞
$$\mathrm{really}? \\ $$$$\mathrm{just}\:\mathrm{try}\:\mathrm{some}\:\mathrm{values}\:\mathrm{with}\:{n}={k}^{\mathrm{2}} \wedge{k}\in\mathbb{N} \\ $$$${y}_{{k}} =\frac{\left(\mathrm{2}{k}^{\mathrm{2}} \right)!}{\mathrm{2}^{{k}} } \\ $$$${y}_{\mathrm{1}} =\mathrm{1} \\ $$$${y}_{\mathrm{2}} =\mathrm{10080} \\ $$$${y}_{\mathrm{3}} =\mathrm{800296713216000} \\ $$$$… \\ $$$${y}_{\mathrm{10}} \approx\mathrm{7}.\mathrm{70}×\mathrm{10}^{\mathrm{371}} \\ $$$$… \\ $$$$\Rightarrow\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:+\infty \\ $$
Commented by liberty last updated on 04/Feb/21
wrong answer 0
$$\mathrm{wrong}\:\mathrm{answer}\:\mathrm{0}\: \\ $$
Answered by mathmax by abdo last updated on 03/Feb/21
u_n =(((2n)!)/2^(√n) ) we have n! ∼n^n e^(−n) (√(2πn))( stirling formula) ⇒ (2n)!∼(2n)^(2n) e^(−2n) (√(4πn)) ⇒u_n ∼((2^(2n) n^(2n) e^(−2n) 2(√(πn)))/2^(√n) ) ⇒ u_n ∼n^(2n) .e^(−2n) .2^(2n−(√n)) (√(πn ))⇒ ln(u_n )=2nln(n)−2n+((n−(√n))ln(2)+(1/2)ln(nπ) ⇒ ln(u_n ) =2n{((ln(n))/(2n))−1 (((n−(√n))ln2)/(2n)) +((ln(nπ))/(4n))}∼2n{−1+(1/2)}∼−n ⇒ lim_(n→+∞) ln(u_n )=−∞ ⇒lim_(n→+∞) u_n =0
$$\mathrm{u}_{\mathrm{n}} =\frac{\left(\mathrm{2n}\right)!}{\mathrm{2}^{\sqrt{\mathrm{n}}} }\:\:\mathrm{we}\:\mathrm{have}\:\:\mathrm{n}!\:\sim\mathrm{n}^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{n}} \sqrt{\mathrm{2}\pi\mathrm{n}}\left(\:\mathrm{stirling}\:\mathrm{formula}\right)\:\Rightarrow \\ $$$$\left(\mathrm{2n}\right)!\sim\left(\mathrm{2n}\right)^{\mathrm{2n}} \:\mathrm{e}^{−\mathrm{2n}} \sqrt{\mathrm{4}\pi\mathrm{n}}\:\Rightarrow\mathrm{u}_{\mathrm{n}} \sim\frac{\mathrm{2}^{\mathrm{2n}} \:\mathrm{n}^{\mathrm{2n}} \:\mathrm{e}^{−\mathrm{2n}} \mathrm{2}\sqrt{\pi\mathrm{n}}}{\mathrm{2}^{\sqrt{\mathrm{n}}} }\:\Rightarrow \\ $$$$\mathrm{u}_{\mathrm{n}} \sim\mathrm{n}^{\mathrm{2n}} \:.\mathrm{e}^{−\mathrm{2n}} \:.\mathrm{2}^{\mathrm{2n}−\sqrt{\mathrm{n}}} \:\sqrt{\pi\mathrm{n}\:}\Rightarrow \\ $$$$\mathrm{ln}\left(\mathrm{u}_{\mathrm{n}} \right)=\mathrm{2nln}\left(\mathrm{n}\right)−\mathrm{2n}+\left(\left(\mathrm{n}−\sqrt{\mathrm{n}}\right)\mathrm{ln}\left(\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{n}\pi\right)\:\Rightarrow\right. \\ $$$$\mathrm{ln}\left(\mathrm{u}_{\mathrm{n}} \right)\:=\mathrm{2n}\left\{\frac{\mathrm{ln}\left(\mathrm{n}\right)}{\mathrm{2n}}−\mathrm{1}\:\frac{\left(\mathrm{n}−\sqrt{\mathrm{n}}\right)\mathrm{ln2}}{\mathrm{2n}}\:+\frac{\mathrm{ln}\left(\mathrm{n}\pi\right)}{\mathrm{4n}}\right\}\sim\mathrm{2n}\left\{−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right\}\sim−\mathrm{n}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{ln}\left(\mathrm{u}_{\mathrm{n}} \right)=−\infty\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{u}_{\mathrm{n}} =\mathrm{0} \\ $$
Answered by liberty last updated on 04/Feb/21
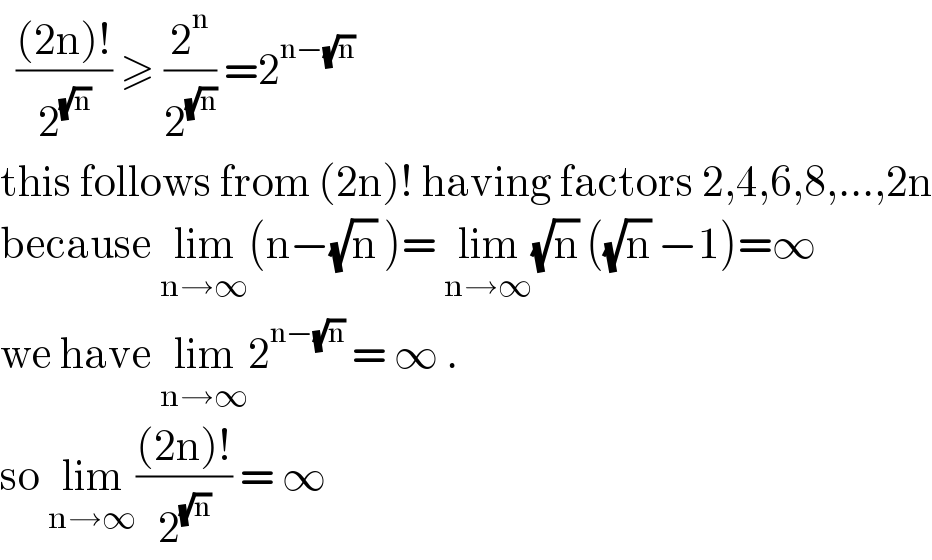
(((2n)!)/2^(√n) ) ≥ (2^n /2^(√n) ) =2^(n−(√n)) this follows from (2n)! having factors 2,4,6,8,...,2n because lim_(n→∞) (n−(√n) )= lim_(n→∞) (√n) ((√n) −1)=∞ we have lim_(n→∞) 2^(n−(√n)) = ∞ . so lim_(n→∞) (((2n)!)/2^(√n) ) = ∞
$$\:\:\frac{\left(\mathrm{2n}\right)!}{\mathrm{2}^{\sqrt{\mathrm{n}}} }\:\geqslant\:\frac{\mathrm{2}^{\mathrm{n}} }{\mathrm{2}^{\sqrt{\mathrm{n}}} }\:=\mathrm{2}^{\mathrm{n}−\sqrt{\mathrm{n}}} \: \\ $$$$\mathrm{this}\:\mathrm{follows}\:\mathrm{from}\:\left(\mathrm{2n}\right)!\:\mathrm{having}\:\mathrm{factors}\:\mathrm{2},\mathrm{4},\mathrm{6},\mathrm{8},…,\mathrm{2n} \\ $$$$\mathrm{because}\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{n}−\sqrt{\mathrm{n}}\:\right)=\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\sqrt{\mathrm{n}}\:\left(\sqrt{\mathrm{n}}\:−\mathrm{1}\right)=\infty \\ $$$$\mathrm{we}\:\mathrm{have}\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}2}^{\mathrm{n}−\sqrt{\mathrm{n}}} \:=\:\infty\:. \\ $$$$\mathrm{so}\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\left(\mathrm{2n}\right)!}{\mathrm{2}^{\sqrt{\mathrm{n}}} }\:=\:\infty\: \\ $$

Pin