Menu Close

Question-131412

Tinku Tara
Pin




Question Number 131412 by mohammad17 last updated on 04/Feb/21
Commented by mohammad17 last updated on 04/Feb/21
bow can solve this
$${bow}\:{can}\:{solve}\:{this} \\ $$
Answered by physicstutes last updated on 04/Feb/21
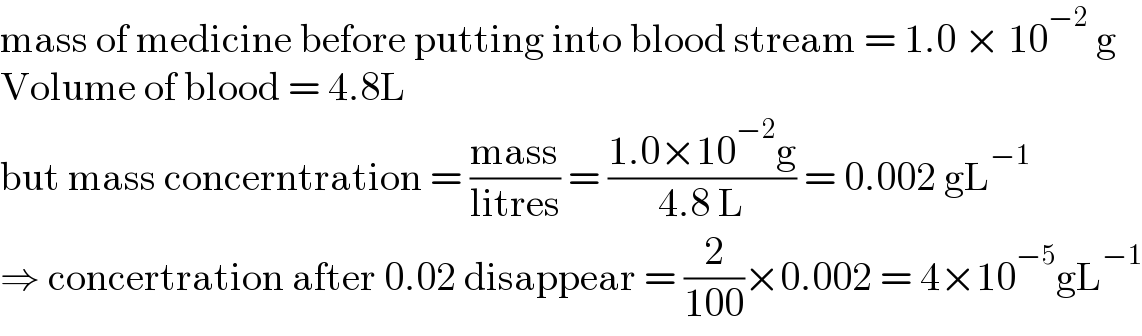
mass of medicine before putting into blood stream = 1.0 × 10^(−2) g Volume of blood = 4.8L but mass concerntration = ((mass)/(litres)) = ((1.0×10^(−2) g)/(4.8 L)) = 0.002 gL^(−1) ⇒ concertration after 0.02 disappear = (2/(100))×0.002 = 4×10^(−5) gL^(−1)
$$\mathrm{mass}\:\mathrm{of}\:\mathrm{medicine}\:\mathrm{before}\:\mathrm{putting}\:\mathrm{into}\:\mathrm{blood}\:\mathrm{stream}\:=\:\mathrm{1}.\mathrm{0}\:×\:\mathrm{10}^{−\mathrm{2}} \:\mathrm{g} \\ $$$$\mathrm{Volume}\:\mathrm{of}\:\mathrm{blood}\:=\:\mathrm{4}.\mathrm{8L} \\ $$$$\mathrm{but}\:\mathrm{mass}\:\mathrm{concerntration}\:=\:\frac{\mathrm{mass}}{\mathrm{litres}}\:=\:\frac{\mathrm{1}.\mathrm{0}×\mathrm{10}^{−\mathrm{2}} \mathrm{g}}{\mathrm{4}.\mathrm{8}\:\mathrm{L}}\:=\:\mathrm{0}.\mathrm{002}\:\mathrm{gL}^{−\mathrm{1}} \\ $$$$\Rightarrow\:\mathrm{concertration}\:\mathrm{after}\:\mathrm{0}.\mathrm{02}\:\mathrm{disappear}\:=\:\frac{\mathrm{2}}{\mathrm{100}}×\mathrm{0}.\mathrm{002}\:=\:\mathrm{4}×\mathrm{10}^{−\mathrm{5}} \mathrm{gL}^{−\mathrm{1}} \\ $$
Commented by mohammad17 last updated on 04/Feb/21
thank you sir can you help me
$${thank}\:{you}\:{sir}\:{can}\:{you}\:{help}\:{me} \\ $$
Commented by mohammad17 last updated on 04/Feb/21
Q/131415
$${Q}/\mathrm{131415} \\ $$

Pin