Question Number 131443 by rs4089 last updated on 04/Feb/21

Answered by Olaf last updated on 05/Feb/21
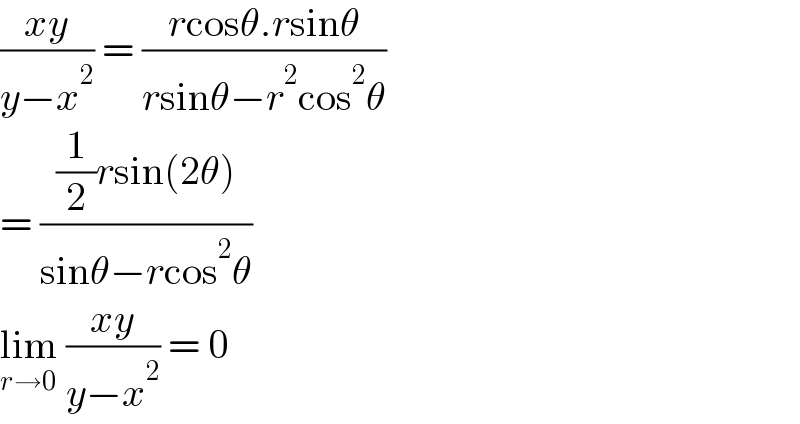
$$\frac{{xy}}{{y}−{x}^{\mathrm{2}} }\:=\:\frac{{r}\mathrm{cos}\theta.{r}\mathrm{sin}\theta}{{r}\mathrm{sin}\theta−{r}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \theta} \\ $$$$=\:\frac{\frac{\mathrm{1}}{\mathrm{2}}{r}\mathrm{sin}\left(\mathrm{2}\theta\right)}{\mathrm{sin}\theta−{r}\mathrm{cos}^{\mathrm{2}} \theta} \\ $$$$\underset{{r}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{xy}}{{y}−{x}^{\mathrm{2}} }\:=\:\mathrm{0} \\ $$
