Question Number 131599 by ajfour last updated on 06/Feb/21

Commented by ajfour last updated on 06/Feb/21
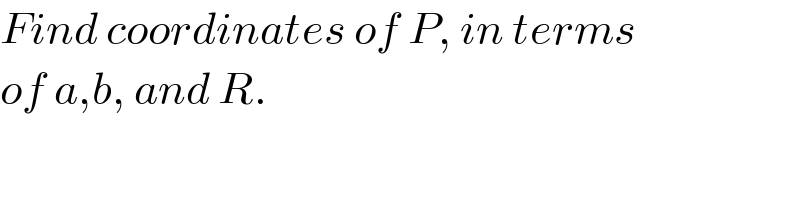
$${Find}\:{coordinates}\:{of}\:{P},\:{in}\:{terms} \\ $$$${of}\:{a},{b},\:{and}\:{R}. \\ $$
Answered by mr W last updated on 06/Feb/21
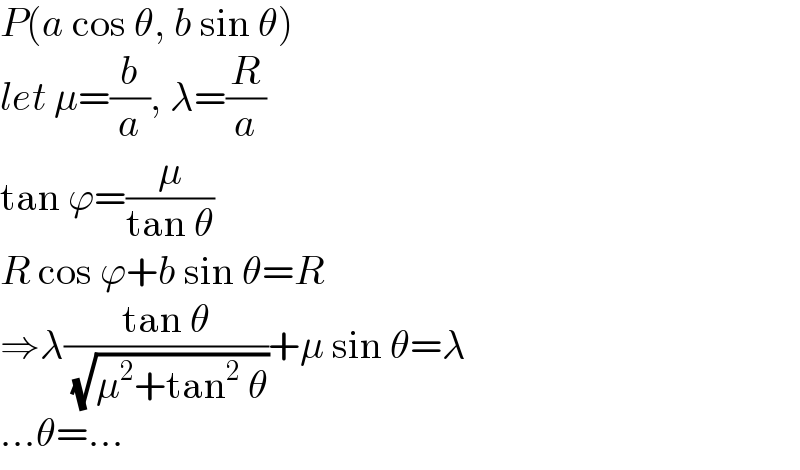
$${P}\left({a}\:\mathrm{cos}\:\theta,\:{b}\:\mathrm{sin}\:\theta\right) \\ $$$${let}\:\mu=\frac{{b}}{{a}},\:\lambda=\frac{{R}}{{a}} \\ $$$$\mathrm{tan}\:\varphi=\frac{\mu}{\mathrm{tan}\:\theta} \\ $$$${R}\:\mathrm{cos}\:\varphi+{b}\:\mathrm{sin}\:\theta={R} \\ $$$$\Rightarrow\lambda\frac{\mathrm{tan}\:\theta}{\:\sqrt{\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\theta}}+\mu\:\mathrm{sin}\:\theta=\lambda \\ $$$$…\theta=… \\ $$
