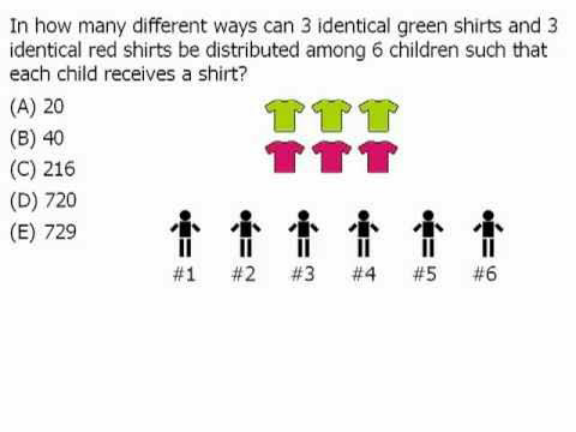
Question Number 131828 by Salman_Abir last updated on 09/Feb/21
Answered by liberty last updated on 09/Feb/21

$$\mathrm{20}\:=\:\frac{\mathrm{6}!}{\mathrm{3}!.\mathrm{3}!} \\ $$
Commented by Salman_Abir last updated on 09/Feb/21

$$\mathrm{detail} \\ $$
Answered by mr W last updated on 09/Feb/21
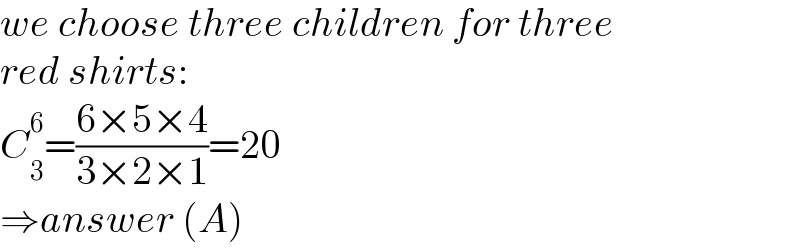
$${we}\:{choose}\:{three}\:{children}\:{for}\:{three} \\ $$$${red}\:{shirts}: \\ $$$${C}_{\mathrm{3}} ^{\mathrm{6}} =\frac{\mathrm{6}×\mathrm{5}×\mathrm{4}}{\mathrm{3}×\mathrm{2}×\mathrm{1}}=\mathrm{20} \\ $$$$\Rightarrow{answer}\:\left({A}\right) \\ $$
Commented by mr W last updated on 09/Feb/21
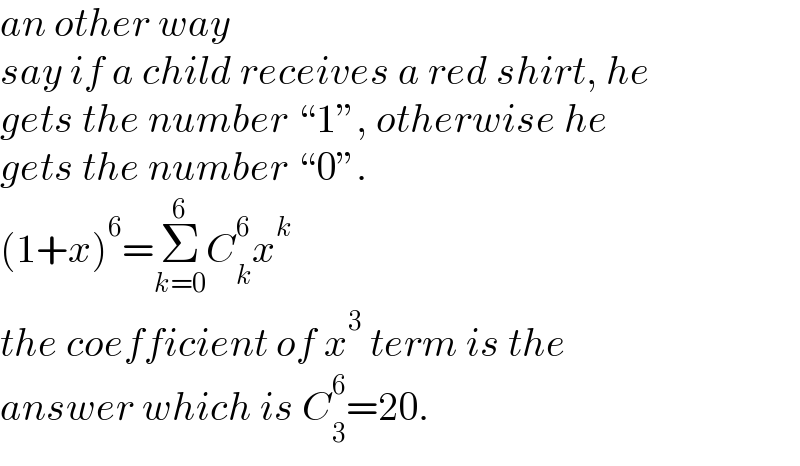
$${an}\:{other}\:{way} \\ $$$${say}\:{if}\:{a}\:{child}\:{receives}\:{a}\:{red}\:{shirt},\:{he} \\ $$$${gets}\:{the}\:{number}\:“\mathrm{1}'',\:{otherwise}\:{he} \\ $$$${gets}\:{the}\:{number}\:“\mathrm{0}''. \\ $$$$\left(\mathrm{1}+{x}\right)^{\mathrm{6}} =\underset{{k}=\mathrm{0}} {\overset{\mathrm{6}} {\sum}}{C}_{{k}} ^{\mathrm{6}} {x}^{{k}} \\ $$$${the}\:{coefficient}\:{of}\:{x}^{\mathrm{3}} \:{term}\:{is}\:{the} \\ $$$${answer}\:{which}\:{is}\:{C}_{\mathrm{3}} ^{\mathrm{6}} =\mathrm{20}. \\ $$
Commented by mr W last updated on 09/Feb/21
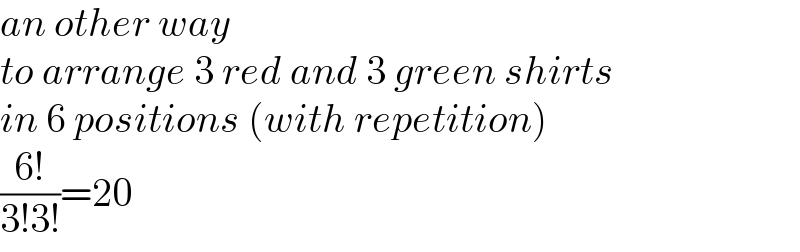
$${an}\:{other}\:{way} \\ $$$${to}\:{arrange}\:\mathrm{3}\:{red}\:{and}\:\mathrm{3}\:{green}\:{shirts} \\ $$$${in}\:\mathrm{6}\:{positions}\:\left({with}\:{repetition}\right) \\ $$$$\frac{\mathrm{6}!}{\mathrm{3}!\mathrm{3}!}=\mathrm{20} \\ $$
Commented by malwan last updated on 09/Feb/21
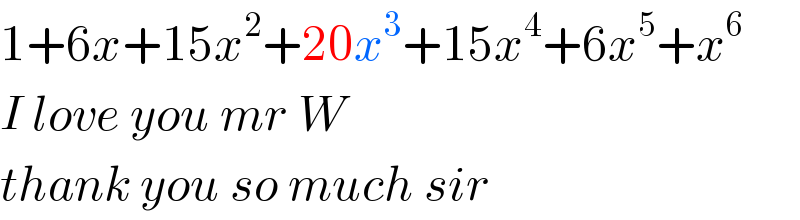
$$\mathrm{1}+\mathrm{6}{x}+\mathrm{15}{x}^{\mathrm{2}} +\mathrm{20}{x}^{\mathrm{3}} +\mathrm{15}{x}^{\mathrm{4}} +\mathrm{6}{x}^{\mathrm{5}} +{x}^{\mathrm{6}} \\ $$$${I}\:{love}\:{you}\:{mr}\:{W} \\ $$$${thank}\:{you}\:{so}\:{much}\:{sir} \\ $$
Commented by mr W last updated on 09/Feb/21
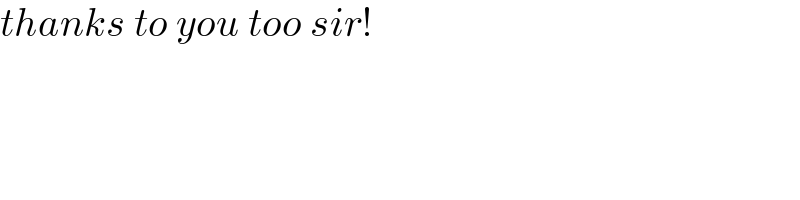
$${thanks}\:{to}\:{you}\:{too}\:{sir}! \\ $$
Commented by Salman_Abir last updated on 09/Feb/21

$$\mathrm{thanks} \\ $$$$ \\ $$
