Menu Close

Question-131887

Tinku Tara 0 Comments
Pin




Question Number 131887 by Algoritm last updated on 09/Feb/21
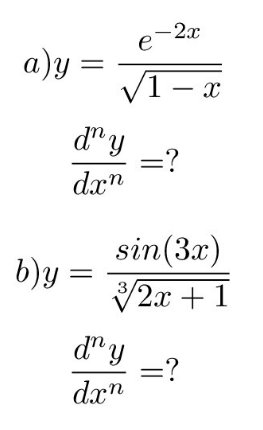
Answered by SEKRET last updated on 09/Feb/21
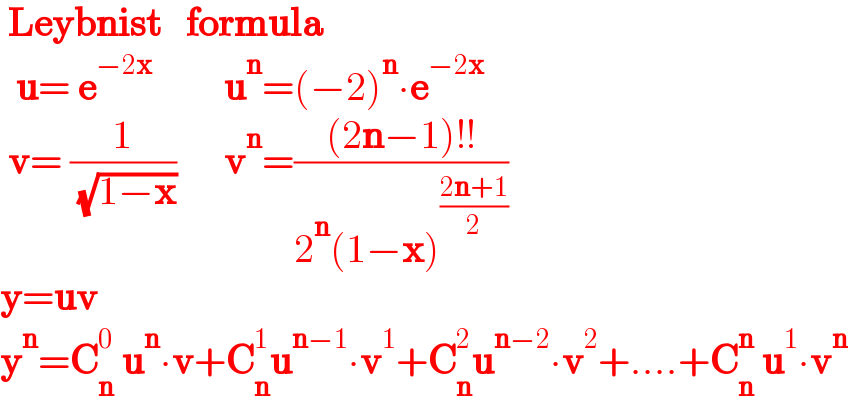
Leybnist formula u= e^(−2x) u^n =(−2)^n ∙e^(−2x) v= (1/( (√(1−x)))) v^n =(((2n−1)!!)/(2^n (1−x)^((2n+1)/2) )) y=uv y^n =C_n ^0 u^n ∙v+C_n ^1 u^(n−1) ∙v^1 +C_n ^2 u^(n−2) ∙v^2 +....+C_n ^n u^1 ∙v^n
$$\:\boldsymbol{\mathrm{Leybnist}}\:\:\:\boldsymbol{\mathrm{formula}} \\ $$$$\:\:\boldsymbol{\mathrm{u}}=\:\boldsymbol{\mathrm{e}}^{−\mathrm{2}\boldsymbol{\mathrm{x}}} \:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{u}}^{\boldsymbol{\mathrm{n}}} =\left(−\mathrm{2}\right)^{\boldsymbol{\mathrm{n}}} \centerdot\boldsymbol{\mathrm{e}}^{−\mathrm{2}\boldsymbol{\mathrm{x}}} \\ $$$$\:\boldsymbol{\mathrm{v}}=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\boldsymbol{\mathrm{x}}}}\:\:\:\:\:\:\boldsymbol{\mathrm{v}}^{\boldsymbol{\mathrm{n}}} =\frac{\left(\mathrm{2}\boldsymbol{\mathrm{n}}−\mathrm{1}\right)!!}{\mathrm{2}^{\boldsymbol{\mathrm{n}}} \left(\mathrm{1}−\boldsymbol{\mathrm{x}}\right)^{\frac{\mathrm{2}\boldsymbol{\mathrm{n}}+\mathrm{1}}{\mathrm{2}}} } \\ $$$$\boldsymbol{\mathrm{y}}=\boldsymbol{\mathrm{uv}} \\ $$$$\boldsymbol{\mathrm{y}}^{\boldsymbol{\mathrm{n}}} =\boldsymbol{\mathrm{C}}_{\boldsymbol{\mathrm{n}}} ^{\mathrm{0}} \:\boldsymbol{\mathrm{u}}^{\boldsymbol{\mathrm{n}}} \centerdot\boldsymbol{\mathrm{v}}+\boldsymbol{\mathrm{C}}_{\boldsymbol{\mathrm{n}}} ^{\mathrm{1}} \boldsymbol{\mathrm{u}}^{\boldsymbol{\mathrm{n}}−\mathrm{1}} \centerdot\boldsymbol{\mathrm{v}}^{\mathrm{1}} +\boldsymbol{\mathrm{C}}_{\boldsymbol{\mathrm{n}}} ^{\mathrm{2}} \boldsymbol{\mathrm{u}}^{\boldsymbol{\mathrm{n}}−\mathrm{2}} \centerdot\boldsymbol{\mathrm{v}}^{\mathrm{2}} +….+\boldsymbol{\mathrm{C}}_{\boldsymbol{\mathrm{n}}} ^{\boldsymbol{\mathrm{n}}} \:\boldsymbol{\mathrm{u}}^{\mathrm{1}} \centerdot\boldsymbol{\mathrm{v}}^{\boldsymbol{\mathrm{n}}} \\ $$
Answered by mathmax by abdo last updated on 10/Feb/21
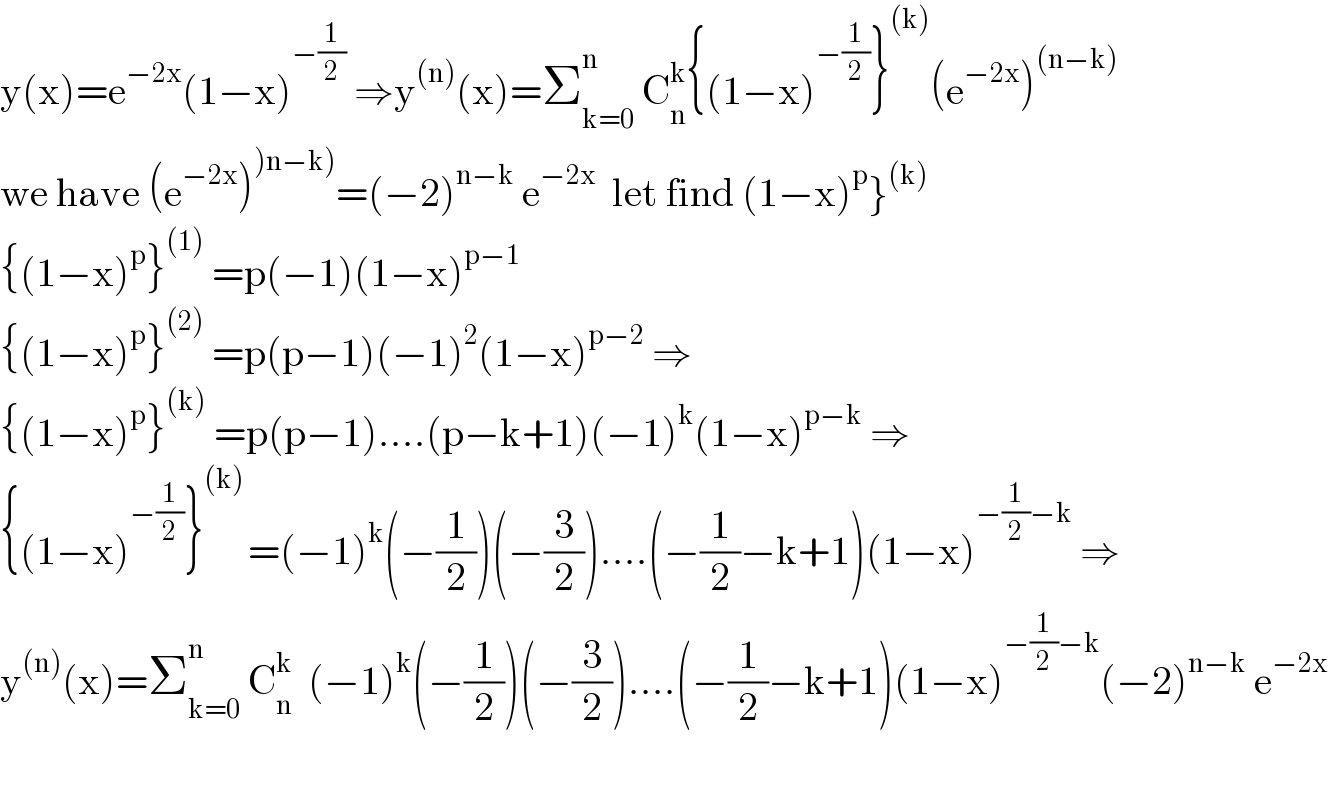
y(x)=e^(−2x) (1−x)^(−(1/2)) ⇒y^((n)) (x)=Σ_(k=0) ^n C_n ^k {(1−x)^(−(1/2)) }^((k)) (e^(−2x) )^((n−k)) we have (e^(−2x) )^()n−k)) =(−2)^(n−k) e^(−2x) let find (1−x)^p }^((k)) {(1−x)^p }^((1)) =p(−1)(1−x)^(p−1) {(1−x)^p }^((2)) =p(p−1)(−1)^2 (1−x)^(p−2) ⇒ {(1−x)^p }^((k)) =p(p−1)....(p−k+1)(−1)^k (1−x)^(p−k) ⇒ {(1−x)^(−(1/2)) }^((k) ) =(−1)^k (−(1/2))(−(3/2))....(−(1/2)−k+1)(1−x)^(−(1/2)−k) ⇒ y^((n)) (x)=Σ_(k=0) ^n C_n ^k (−1)^k (−(1/2))(−(3/2))....(−(1/2)−k+1)(1−x)^(−(1/2)−k) (−2)^(n−k) e^(−2x)
$$\mathrm{y}\left(\mathrm{x}\right)=\mathrm{e}^{−\mathrm{2x}} \left(\mathrm{1}−\mathrm{x}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\Rightarrow\mathrm{y}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \left\{\left(\mathrm{1}−\mathrm{x}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \right\}^{\left(\mathrm{k}\right)} \left(\mathrm{e}^{−\mathrm{2x}} \right)^{\left(\mathrm{n}−\mathrm{k}\right)} \\ $$$$\left.\mathrm{we}\:\mathrm{have}\:\left(\mathrm{e}^{−\mathrm{2x}} \right)^{\left.\right)\left.\mathrm{n}−\mathrm{k}\right)} =\left(−\mathrm{2}\right)^{\mathrm{n}−\mathrm{k}} \:\mathrm{e}^{−\mathrm{2x}} \:\:\mathrm{let}\:\mathrm{find}\:\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{p}} \right\}^{\left(\mathrm{k}\right)} \\ $$$$\left\{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{p}} \right\}^{\left(\mathrm{1}\right)} \:=\mathrm{p}\left(−\mathrm{1}\right)\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{p}−\mathrm{1}} \\ $$$$\left\{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{p}} \right\}^{\left(\mathrm{2}\right)} \:=\mathrm{p}\left(\mathrm{p}−\mathrm{1}\right)\left(−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{p}−\mathrm{2}} \:\Rightarrow \\ $$$$\left\{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{p}} \right\}^{\left(\mathrm{k}\right)} \:=\mathrm{p}\left(\mathrm{p}−\mathrm{1}\right)….\left(\mathrm{p}−\mathrm{k}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{\mathrm{k}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{p}−\mathrm{k}} \:\Rightarrow \\ $$$$\left\{\left(\mathrm{1}−\mathrm{x}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \right\}^{\left(\mathrm{k}\right)\:} =\left(−\mathrm{1}\right)^{\mathrm{k}} \left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)….\left(−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{k}+\mathrm{1}\right)\left(\mathrm{1}−\mathrm{x}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{k}} \:\Rightarrow \\ $$$$\mathrm{y}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\:\left(−\mathrm{1}\right)^{\mathrm{k}} \left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)….\left(−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{k}+\mathrm{1}\right)\left(\mathrm{1}−\mathrm{x}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{k}} \left(−\mathrm{2}\right)^{\mathrm{n}−\mathrm{k}} \:\mathrm{e}^{−\mathrm{2x}} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *