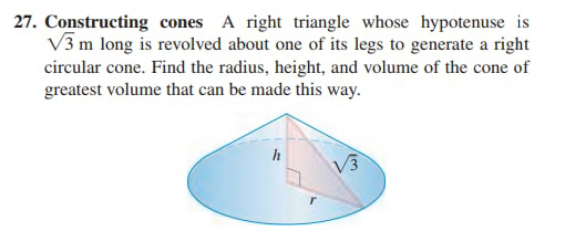
Question Number 131960 by liberty last updated on 10/Feb/21
Answered by mr W last updated on 10/Feb/21
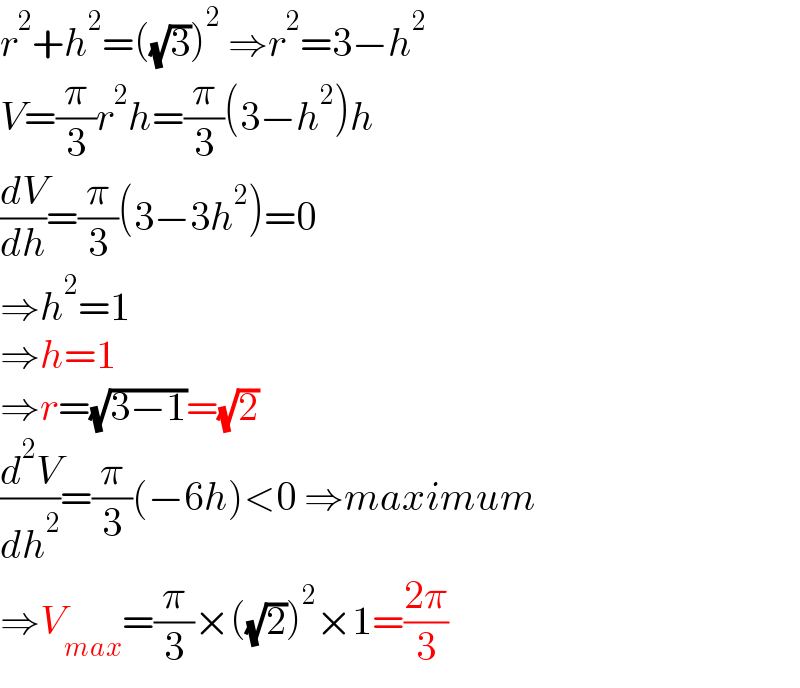
$${r}^{\mathrm{2}} +{h}^{\mathrm{2}} =\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \:\Rightarrow{r}^{\mathrm{2}} =\mathrm{3}−{h}^{\mathrm{2}} \\ $$$${V}=\frac{\pi}{\mathrm{3}}{r}^{\mathrm{2}} {h}=\frac{\pi}{\mathrm{3}}\left(\mathrm{3}−{h}^{\mathrm{2}} \right){h} \\ $$$$\frac{{dV}}{{dh}}=\frac{\pi}{\mathrm{3}}\left(\mathrm{3}−\mathrm{3}{h}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow{h}^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow{h}=\mathrm{1} \\ $$$$\Rightarrow{r}=\sqrt{\mathrm{3}−\mathrm{1}}=\sqrt{\mathrm{2}} \\ $$$$\frac{{d}^{\mathrm{2}} {V}}{{dh}^{\mathrm{2}} }=\frac{\pi}{\mathrm{3}}\left(−\mathrm{6}{h}\right)<\mathrm{0}\:\Rightarrow{maximum} \\ $$$$\Rightarrow{V}_{{max}} =\frac{\pi}{\mathrm{3}}×\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} ×\mathrm{1}=\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$
Commented by otchereabdullai@gmail.com last updated on 10/Feb/21

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{prorW} \\ $$
Commented by liberty last updated on 10/Feb/21

$$\mathrm{nice} \\ $$
