Question Number 132433 by john_santu last updated on 14/Feb/21
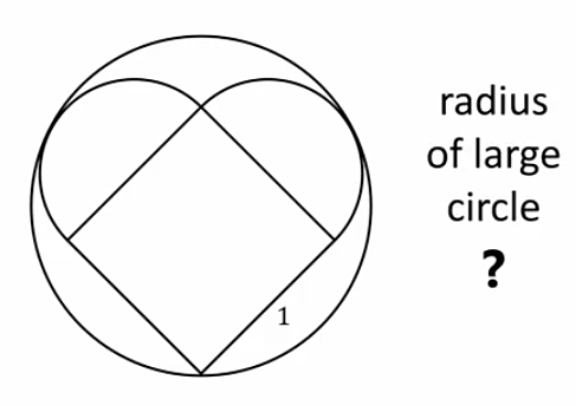
Answered by liberty last updated on 14/Feb/21
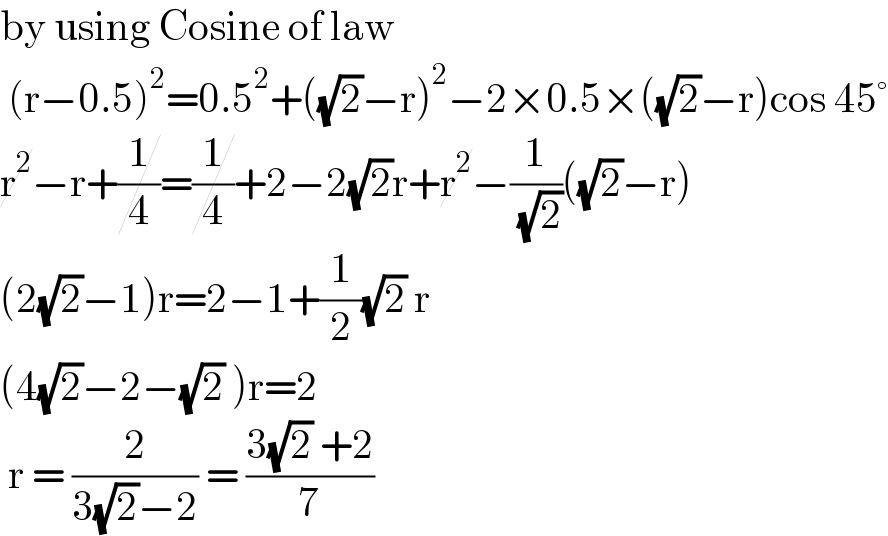
$$\mathrm{by}\:\mathrm{using}\:\mathrm{Cosine}\:\mathrm{of}\:\mathrm{law}\: \\ $$$$\:\left(\mathrm{r}−\mathrm{0}.\mathrm{5}\right)^{\mathrm{2}} =\mathrm{0}.\mathrm{5}^{\mathrm{2}} +\left(\sqrt{\mathrm{2}}−\mathrm{r}\right)^{\mathrm{2}} −\mathrm{2}×\mathrm{0}.\mathrm{5}×\left(\sqrt{\mathrm{2}}−\mathrm{r}\right)\mathrm{cos}\:\mathrm{45}° \\ $$$$\cancel{\mathrm{r}^{\mathrm{2}} }−\mathrm{r}+\cancel{\frac{\mathrm{1}}{\mathrm{4}}}=\cancel{\frac{\mathrm{1}}{\mathrm{4}}}+\mathrm{2}−\mathrm{2}\sqrt{\mathrm{2}}\mathrm{r}+\cancel{\mathrm{r}^{\mathrm{2}} }−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\sqrt{\mathrm{2}}−\mathrm{r}\right) \\ $$$$\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}\right)\mathrm{r}=\mathrm{2}−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}}\:\mathrm{r} \\ $$$$\left(\mathrm{4}\sqrt{\mathrm{2}}−\mathrm{2}−\sqrt{\mathrm{2}}\:\right)\mathrm{r}=\mathrm{2} \\ $$$$\:\mathrm{r}\:=\:\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{2}}−\mathrm{2}}\:=\:\frac{\mathrm{3}\sqrt{\mathrm{2}}\:+\mathrm{2}}{\mathrm{7}} \\ $$
