Question Number 132564 by abony1303 last updated on 15/Feb/21

Answered by abony1303 last updated on 15/Feb/21

$$\mathrm{pls}\:\mathrm{help}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{shaded}\:\mathrm{region} \\ $$
Answered by MJS_new last updated on 15/Feb/21
![rotate the picture by −45° ⇒ big upper half circle y=(√(100−x^2 )) small upper half circle y=5(√2)+(√(25−x^2 )) they intersect at x=±((5(√(14)))/4) (1/4) of blue region ∫_0 ^((5(√(14)))/4) (5(√2)+(√(25−x^2 ))−(√(100−x^2 )))dx= =[5(√2)x+((x(√(25−x^2 )))/2)+((25arcsin (x/5))/2)−((x(√(100−x^2 )))/2)−50arcsin (x/(10))]_0 ^((5(√(14)))/4) = =((25)/4)((√7)+2arcsin ((√(14))/4) −8arcsin ((√(14))/8))= =((25)/4)((√7)−arctan ((1541(√7))/(393)))≈7.31906 ⇒ blue area =25((√7)−arctan ((1541(√7))/(393)))≈29.2763](https://www.tinkutara.com/question/Q132571.png)
$$\mathrm{rotate}\:\mathrm{the}\:\mathrm{picture}\:\mathrm{by}\:−\mathrm{45}° \\ $$$$\Rightarrow \\ $$$$\mathrm{big}\:\mathrm{upper}\:\mathrm{half}\:\mathrm{circle} \\ $$$${y}=\sqrt{\mathrm{100}−{x}^{\mathrm{2}} } \\ $$$$\mathrm{small}\:\mathrm{upper}\:\mathrm{half}\:\mathrm{circle} \\ $$$${y}=\mathrm{5}\sqrt{\mathrm{2}}+\sqrt{\mathrm{25}−{x}^{\mathrm{2}} } \\ $$$$\mathrm{they}\:\mathrm{intersect}\:\mathrm{at}\:{x}=\pm\frac{\mathrm{5}\sqrt{\mathrm{14}}}{\mathrm{4}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{of}\:\mathrm{blue}\:\mathrm{region} \\ $$$$\underset{\mathrm{0}} {\overset{\frac{\mathrm{5}\sqrt{\mathrm{14}}}{\mathrm{4}}} {\int}}\left(\mathrm{5}\sqrt{\mathrm{2}}+\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }−\sqrt{\mathrm{100}−{x}^{\mathrm{2}} }\right){dx}= \\ $$$$=\left[\mathrm{5}\sqrt{\mathrm{2}}{x}+\frac{{x}\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }}{\mathrm{2}}+\frac{\mathrm{25arcsin}\:\frac{{x}}{\mathrm{5}}}{\mathrm{2}}−\frac{{x}\sqrt{\mathrm{100}−{x}^{\mathrm{2}} }}{\mathrm{2}}−\mathrm{50arcsin}\:\frac{{x}}{\mathrm{10}}\right]_{\mathrm{0}} ^{\frac{\mathrm{5}\sqrt{\mathrm{14}}}{\mathrm{4}}} = \\ $$$$=\frac{\mathrm{25}}{\mathrm{4}}\left(\sqrt{\mathrm{7}}+\mathrm{2arcsin}\:\frac{\sqrt{\mathrm{14}}}{\mathrm{4}}\:−\mathrm{8arcsin}\:\frac{\sqrt{\mathrm{14}}}{\mathrm{8}}\right)= \\ $$$$=\frac{\mathrm{25}}{\mathrm{4}}\left(\sqrt{\mathrm{7}}−\mathrm{arctan}\:\frac{\mathrm{1541}\sqrt{\mathrm{7}}}{\mathrm{393}}\right)\approx\mathrm{7}.\mathrm{31906} \\ $$$$\Rightarrow\:\mathrm{blue}\:\mathrm{area}\:=\mathrm{25}\left(\sqrt{\mathrm{7}}−\mathrm{arctan}\:\frac{\mathrm{1541}\sqrt{\mathrm{7}}}{\mathrm{393}}\right)\approx\mathrm{29}.\mathrm{2763} \\ $$
Commented by mr W last updated on 15/Feb/21

$${i}\:{think}\:{this}\:{is}\:{the}\:{best}\:{path}. \\ $$
Answered by mr W last updated on 15/Feb/21

Commented by mr W last updated on 15/Feb/21
![cos α=(((2r)^2 +((√2)r)^2 −r^2 )/(2×2r×(√2)r))=((5(√2))/8) cos γ=(((2r)^2 +r^2 −((√2)r)^2 )/(2×2r×r))=(3/4) β=α+γ orange shaded segment: A_(Or) =(r^2 /2)(2β−sin 2β) green shaded segment: A_(Gr) =(((2r)^2 )/2)(2α−sin 2α) blue shaded area: A_(blue) =2(A_(Or) −A_(Gr) ) =[2β−sin 2β−8α+4sin 2α]r^2 =[10α+2γ−sin (2α+2γ)+4sin 2α]r^2 =[10α+2γ+sin 2α(4−cos 2γ)−cos 2α sin 2γ]r^2 =2[γ−3α+sin α cos α (5−2 cos^2 γ)−(2 cos^2 α−1)sin γ cos γ]r^2 =2[γ−3α+((√(14))/8)×((5(√2))/8)(5−2×(3^2 /4^2 ))−(2×((25×2)/(64))−1)×((√7)/4)×(3/4)]r^2 =2(γ−3α+((√7)/2))r^2 =2(cos^(−1) (3/4)−3 cos^(−1) ((5(√2))/8)+((√7)/2))r^2 ≈1.171 050 076 r^2 ≈29.276 252](https://www.tinkutara.com/question/Q132581.png)
$$\mathrm{cos}\:\alpha=\frac{\left(\mathrm{2}{r}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{2}}{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }{\mathrm{2}×\mathrm{2}{r}×\sqrt{\mathrm{2}}{r}}=\frac{\mathrm{5}\sqrt{\mathrm{2}}}{\mathrm{8}} \\ $$$$\mathrm{cos}\:\gamma=\frac{\left(\mathrm{2}{r}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} −\left(\sqrt{\mathrm{2}}{r}\right)^{\mathrm{2}} }{\mathrm{2}×\mathrm{2}{r}×{r}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\beta=\alpha+\gamma \\ $$$${orange}\:{shaded}\:{segment}: \\ $$$${A}_{{Or}} =\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{2}\beta−\mathrm{sin}\:\mathrm{2}\beta\right) \\ $$$${green}\:{shaded}\:{segment}: \\ $$$${A}_{{Gr}} =\frac{\left(\mathrm{2}{r}\right)^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{2}\alpha−\mathrm{sin}\:\mathrm{2}\alpha\right) \\ $$$${blue}\:{shaded}\:{area}: \\ $$$${A}_{{blue}} =\mathrm{2}\left({A}_{{Or}} −{A}_{{Gr}} \right) \\ $$$$=\left[\mathrm{2}\beta−\mathrm{sin}\:\mathrm{2}\beta−\mathrm{8}\alpha+\mathrm{4sin}\:\mathrm{2}\alpha\right]{r}^{\mathrm{2}} \\ $$$$=\left[\mathrm{10}\alpha+\mathrm{2}\gamma−\mathrm{sin}\:\left(\mathrm{2}\alpha+\mathrm{2}\gamma\right)+\mathrm{4sin}\:\mathrm{2}\alpha\right]{r}^{\mathrm{2}} \\ $$$$=\left[\mathrm{10}\alpha+\mathrm{2}\gamma+\mathrm{sin}\:\mathrm{2}\alpha\left(\mathrm{4}−\mathrm{cos}\:\mathrm{2}\gamma\right)−\mathrm{cos}\:\mathrm{2}\alpha\:\mathrm{sin}\:\mathrm{2}\gamma\right]{r}^{\mathrm{2}} \\ $$$$=\mathrm{2}\left[\gamma−\mathrm{3}\alpha+\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha\:\left(\mathrm{5}−\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\gamma\right)−\left(\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\alpha−\mathrm{1}\right)\mathrm{sin}\:\gamma\:\mathrm{cos}\:\gamma\right]{r}^{\mathrm{2}} \\ $$$$=\mathrm{2}\left[\gamma−\mathrm{3}\alpha+\frac{\sqrt{\mathrm{14}}}{\mathrm{8}}×\frac{\mathrm{5}\sqrt{\mathrm{2}}}{\mathrm{8}}\left(\mathrm{5}−\mathrm{2}×\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{4}^{\mathrm{2}} }\right)−\left(\mathrm{2}×\frac{\mathrm{25}×\mathrm{2}}{\mathrm{64}}−\mathrm{1}\right)×\frac{\sqrt{\mathrm{7}}}{\mathrm{4}}×\frac{\mathrm{3}}{\mathrm{4}}\right]{r}^{\mathrm{2}} \\ $$$$=\mathrm{2}\left(\gamma−\mathrm{3}\alpha+\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\right){r}^{\mathrm{2}} \\ $$$$=\mathrm{2}\left(\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{4}}−\mathrm{3}\:\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{5}\sqrt{\mathrm{2}}}{\mathrm{8}}+\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\right){r}^{\mathrm{2}} \\ $$$$\approx\mathrm{1}.\mathrm{171}\:\mathrm{050}\:\mathrm{076}\:{r}^{\mathrm{2}} \approx\mathrm{29}.\mathrm{276}\:\mathrm{252} \\ $$
Commented by Tawa11 last updated on 06/Nov/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 15/Feb/21
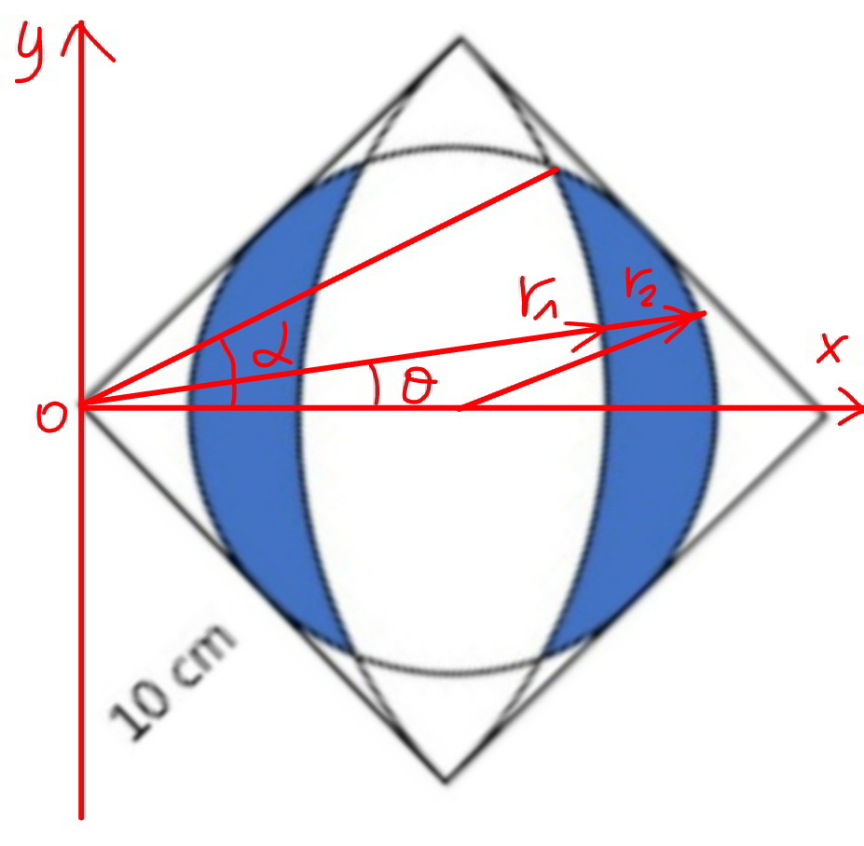
Commented by mr W last updated on 15/Feb/21
![r_1 =a=2r=10 r^2 =r_2 ^2 +((√2)r)^2 −2r_2 (√2)r cos θ r_2 ^2 −2(√2)cos θ rr_2 +r^2 =0 r_2 =r((√2)cos θ+(√(cos 2θ))) r((√2)cos α+(√(cos 2α)))=2r (√(cos 2α))=2−(√2)cos α cos 2α=4−4(√2)cos α+2 cos^2 θ cos α=((5(√2))/8) (1/4)A_(blue) =∫_0 ^α (((r_2 ^2 −r_1 ^2 )dθ)/2) A_(blue) =2∫_0 ^α (r_2 ^2 −r_1 ^2 )dθ =2r^2 ∫_0 ^α [((√2)cos θ+(√(cos 2θ)))^2 −4]dθ =2r^2 ∫_0 ^α (2cos^2 θ+cos 2θ+2cos θ(√(2 cos 2θ))−4)dθ =2r^2 ∫_0 ^α (2 cos 2θ+2cos θ(√(2(1−2sin^2 θ)))−3)dθ =2r^2 [sin 2θ−3θ+sin^(−1) ((√2) sin θ)+(√2)sin θ(√(2 cos^2 θ−1))]_0 ^α =2r^2 [sin 2α−3α+sin^(−1) ((√2) sin α)+(√2)sin α(√(2 cos^2 α−1))] =2r^2 [((5(√7))/(16))−3cos^(−1) ((5(√2))/8)+sin^(−1) ((√7)/4)+((3(√7))/(16))] =[(√7)−6cos^(−1) ((5(√2))/8)+2 sin^(−1) ((√7)/4)]r^2 =1.171 050 r^2 =29.276 252](https://www.tinkutara.com/question/Q132605.png)
$${r}_{\mathrm{1}} ={a}=\mathrm{2}{r}=\mathrm{10} \\ $$$${r}^{\mathrm{2}} ={r}_{\mathrm{2}} ^{\mathrm{2}} +\left(\sqrt{\mathrm{2}}{r}\right)^{\mathrm{2}} −\mathrm{2}{r}_{\mathrm{2}} \sqrt{\mathrm{2}}{r}\:\mathrm{cos}\:\theta \\ $$$${r}_{\mathrm{2}} ^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}\mathrm{cos}\:\theta\:{rr}_{\mathrm{2}} +{r}^{\mathrm{2}} =\mathrm{0} \\ $$$${r}_{\mathrm{2}} ={r}\left(\sqrt{\mathrm{2}}\mathrm{cos}\:\theta+\sqrt{\mathrm{cos}\:\mathrm{2}\theta}\right) \\ $$$${r}\left(\sqrt{\mathrm{2}}\mathrm{cos}\:\alpha+\sqrt{\mathrm{cos}\:\mathrm{2}\alpha}\right)=\mathrm{2}{r} \\ $$$$\sqrt{\mathrm{cos}\:\mathrm{2}\alpha}=\mathrm{2}−\sqrt{\mathrm{2}}\mathrm{cos}\:\alpha \\ $$$$\mathrm{cos}\:\mathrm{2}\alpha=\mathrm{4}−\mathrm{4}\sqrt{\mathrm{2}}\mathrm{cos}\:\alpha+\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\theta \\ $$$$\mathrm{cos}\:\alpha=\frac{\mathrm{5}\sqrt{\mathrm{2}}}{\mathrm{8}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}{A}_{{blue}} =\int_{\mathrm{0}} ^{\alpha} \frac{\left({r}_{\mathrm{2}} ^{\mathrm{2}} −{r}_{\mathrm{1}} ^{\mathrm{2}} \right){d}\theta}{\mathrm{2}} \\ $$$${A}_{{blue}} =\mathrm{2}\int_{\mathrm{0}} ^{\alpha} \left({r}_{\mathrm{2}} ^{\mathrm{2}} −{r}_{\mathrm{1}} ^{\mathrm{2}} \right){d}\theta \\ $$$$=\mathrm{2}{r}^{\mathrm{2}} \int_{\mathrm{0}} ^{\alpha} \left[\left(\sqrt{\mathrm{2}}\mathrm{cos}\:\theta+\sqrt{\mathrm{cos}\:\mathrm{2}\theta}\right)^{\mathrm{2}} −\mathrm{4}\right]{d}\theta \\ $$$$=\mathrm{2}{r}^{\mathrm{2}} \int_{\mathrm{0}} ^{\alpha} \left(\mathrm{2cos}^{\mathrm{2}} \:\theta+\mathrm{cos}\:\mathrm{2}\theta+\mathrm{2cos}\:\theta\sqrt{\mathrm{2}\:\mathrm{cos}\:\mathrm{2}\theta}−\mathrm{4}\right){d}\theta \\ $$$$=\mathrm{2}{r}^{\mathrm{2}} \int_{\mathrm{0}} ^{\alpha} \left(\mathrm{2}\:\mathrm{cos}\:\mathrm{2}\theta+\mathrm{2cos}\:\theta\sqrt{\mathrm{2}\left(\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \:\theta\right)}−\mathrm{3}\right){d}\theta \\ $$$$=\mathrm{2}{r}^{\mathrm{2}} \left[\mathrm{sin}\:\mathrm{2}\theta−\mathrm{3}\theta+\mathrm{sin}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}\:\mathrm{sin}\:\theta\right)+\sqrt{\mathrm{2}}\mathrm{sin}\:\theta\sqrt{\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{1}}\right]_{\mathrm{0}} ^{\alpha} \\ $$$$=\mathrm{2}{r}^{\mathrm{2}} \left[\mathrm{sin}\:\mathrm{2}\alpha−\mathrm{3}\alpha+\mathrm{sin}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}\:\mathrm{sin}\:\alpha\right)+\sqrt{\mathrm{2}}\mathrm{sin}\:\alpha\sqrt{\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\alpha−\mathrm{1}}\right] \\ $$$$=\mathrm{2}{r}^{\mathrm{2}} \left[\frac{\mathrm{5}\sqrt{\mathrm{7}}}{\mathrm{16}}−\mathrm{3cos}^{−\mathrm{1}} \frac{\mathrm{5}\sqrt{\mathrm{2}}}{\mathrm{8}}+\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{7}}}{\mathrm{4}}+\frac{\mathrm{3}\sqrt{\mathrm{7}}}{\mathrm{16}}\right] \\ $$$$=\left[\sqrt{\mathrm{7}}−\mathrm{6cos}^{−\mathrm{1}} \frac{\mathrm{5}\sqrt{\mathrm{2}}}{\mathrm{8}}+\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{7}}}{\mathrm{4}}\right]{r}^{\mathrm{2}} \\ $$$$=\mathrm{1}.\mathrm{171}\:\mathrm{050}\:{r}^{\mathrm{2}} =\mathrm{29}.\mathrm{276}\:\mathrm{252} \\ $$
